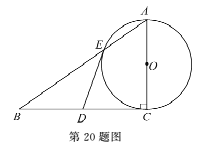
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】:
试题分析:利用思路:知(连)半径,证垂直,证明DE是圆O的切线;利用射影定理或相似三角形证明:BE2=BE×BA,再列方程,求AE的长.
试题解析:(1)如图所示,连接OE,CE
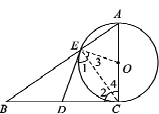
∵AC是圆O的直径
∴∠AEC=∠BEC=90°
∵D是BC的中点
∴ED=![]() BC=DC
BC=DC
∴∠1=∠2
∵OE=OC
∴∠3=∠4
∴∠1+∠3=∠2+∠4,即∠OED=∠ACD
∵∠ACD=90°
∴∠OED=90°,即OE⊥DE
又∵E是圆O上的一点
∴DE是圆O的切线.
(2)由(1)知∠BEC=90°
在RtΔBEC与RtΔBCA中,∠B为公共角,
∴ΔBEC∽ΔBCA
∴![]()
即BC2=BE×BA
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x.
又∵BC=6
∴62=2x×3x
∴x=![]() ,即AE=
,即AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中
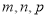 的值,并补全条形统计图;
的值,并补全条形统计图;(3)若该中学约有
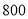 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
求证:直线AD是线段CE的垂直平分线.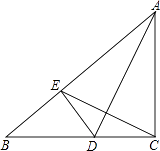
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高
 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心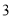 米.
米.
(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户
种植A类蔬菜面积
(单位:亩)种植B类蔬菜面积
(单位:亩)总收入
(单位:元)甲
3
1
12500
乙
2
3
16500
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续
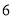 天的最低气温(单位:℃):
天的最低气温(单位:℃):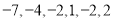 .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )A.平均数是
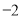 B.中位数是
B.中位数是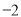 C.众数是
C.众数是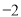 D.方差是
D.方差是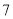
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合:
(1)在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系. 小亮同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF、FD之间的数量关系.请你按照小亮的思路写出推理过程.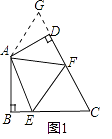
(2)如图2,已知正方形ABCD,△AEF是正方形ABCD的内接等边三角形,请你找出S△ABE、S△ADF、S△CEF之间的数量关系,并说明理由.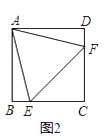
相关试题

