【题目】销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.
(1)求A、B两种型号的轿车每辆分别多少元?
(2)若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?
参考答案:
【答案】
(1)解:设A型轿车每辆x万元,B型轿车每辆y万元.
根据题意,可得 ![]() ,解得:
,解得: ![]() ,
,
15万元=150000元,10万元=100000元.
答:所以A型轿车每辆150000元,B型轿车每辆100000元.
(2)解:设购进A型轿车a辆,则B型轿车(30﹣a)辆.
根据题意,得 ![]() ,解这个不等式组,得18≤a≤20.
,解这个不等式组,得18≤a≤20.
因为a为整数,所以a=18,19,20.
30﹣a的值分别是12,11,10.
因此有三种购车方案:方案一:购进A型轿车18辆,B型轿车12辆;方案二:购进A型轿车19辆,B型轿车11辆;方案三:购进A型轿车20辆,B型轿车10辆.
方案一获利:18×0.8+12×0.5=20.4(万元);
方案二获利:19×0.8+11×0.5=20.7(万元);
方案三获利:20×0.8+10×0.5=21(万元).
【解析】(1)等量关系为:10辆A型轿车总价钱+15辆B型轿车总价钱=300;8辆A型轿车总价钱+18辆B型轿车总价钱=300,把相关数值代入计算即可;(2)关系式为:A型轿车总价钱+B型轿车总价钱≤400;A型轿车总利润+B型轿车总利润≥20.4,求合适的正整数解即可.
【考点精析】根据题目的已知条件,利用一元一次不等式组的应用的相关知识可以得到问题的答案,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
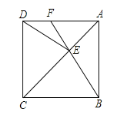
查看答案和解析>>【题目】如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140,求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若AB∥CD,AB∥EF,则CD_______EF,其理由是_______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.
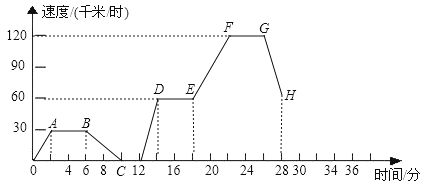
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
(2)汽车在点A的速度是多少?在点C呢?
(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某城市,80%的家庭年收入不少于2.5万元,下面一定不少于2.5万元的是( )
A. 年收入的平均数 B. 年收入的众数
C. 年收入的中位数 D. 年收入的平均数和众数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2x2﹣x2=2
B.5c2+5d2=5c2d2
C.5xy﹣4xy=xy
D.2m2+3m3=5m5 -
科目: 来源: 题型:
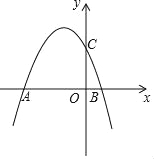
查看答案和解析>>【题目】如图,二次函数y=ax2﹣
 x+2(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
相关试题

