【题目】如图,在Rt△ABC中,∠C=90,AC=6,BC=8,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点D从点A开始,沿边AB向点B以每秒![]() 个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
(1)当t为何值时,四边形BQPD的面积为△ABC面积的![]() ?
?
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度。

参考答案:
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)不存在;当点Q的速度为每秒
;(3)不存在;当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.
秒,四边形PDBQ是菱形.
【解析】
(1)首先表示出四边形面积以及求出三角形面积,列方程求解即可;
(2)由BQ//DP,可得当BQ=DP时,四边形PDBQ是平行四边形,由此可得关于t的方程,解方程即可得;
(3)利用(2)中所求,即可求得此时DP与BD的长,由DP≠BD,可判定平行四边形PDBQ不能为菱形,然后设点Q的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD=BQ,列方程求解即可.
(1)∵直线PD⊥AC,
∴∠APD=90°,
又∵∠C=90°,
∴∠C=∠APD,
∴PD//BC,
在Rt△APD中,AD=![]() ,AP=t,
,AP=t,
∴PD=![]() ,PC=AC-AP=6-t,
,PC=AC-AP=6-t,
∵CQ=2t,BC=8,
∴BQ=8-2t,
∴四边形BQPD的面积为:![]() (BQ+DP)×PC=
(BQ+DP)×PC=![]() (8-2t+
(8-2t+![]() t)(6-t),
t)(6-t),
△ABC的面积为:![]() ACBC=
ACBC=![]() ×6×8=24,
×6×8=24,
∴四边形BQPD的面积为△ABC面积的![]() 时,
时,![]() ×24=
×24=![]() (8-2t+
(8-2t+![]() t)(6-t),
t)(6-t),
解得:![]() ,
,
∵当其中一点到达端点时,另两个点也随之停止运动,
∴t≤4,
∴![]() 不合题意,舍去,
不合题意,舍去,
∴当t为![]() 时,四边形BQPD的面积为△ABC面积的
时,四边形BQPD的面积为△ABC面积的![]() ;
;
(2)存在,
∵PD//BC,
∴BQ//DP,
∴当BQ=DP时,四边形PDBQ是行四边形,
即8-2t=![]() ,解得:t=
,解得:t=![]() ,
,
∴存在,t=![]() 时,四边形PDBQ为平行四边形;
时,四边形PDBQ为平行四边形;
(3)不存在,理由如下:
当![]() 时,
时,![]() ,
,
∴DP≠BD,
∴平行四边形PDBQ不能为菱形;
设点Q的速度为每秒v个单位长度,
则BQ=8-vt,PD=![]() ,BD=10-
,BD=10-![]() ,
,
要使四边形PDBQ成为菱形,则PD=BD=BQ,
当PD=BD时,即![]() ,解得:t=
,解得:t=![]() ,
,
当PD=BQ,t=![]() 时,即
时,即![]() ,解得:v=
,解得:v=![]() ,
,
所以当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.
秒,四边形PDBQ是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
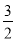 ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.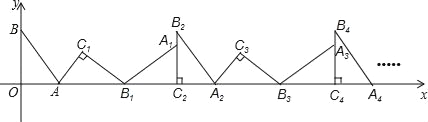
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足
 +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.

-
科目: 来源: 题型:
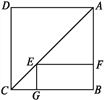
查看答案和解析>>【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费,用水不超过7吨,按每吨1.5元收费;若超过7吨,未超过部分仍按每吨1.5元收取,而超过部分则按每吨2.3元收费.
(1)如果某用户5月份水费平均为每吨1.6元,那么该用户5月份应交水费多少元?
(2)如果某用户5月份交水费17.4元,那么该用户5月份水费平均每吨多少元?
相关试题

