【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 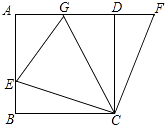
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
参考答案:
【答案】
(1)证明:在正方形ABCD中,
∵ 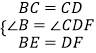 ,
,
∴△CBE≌△CDF(SAS).
∴CE=CF
(2)解:GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵ 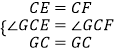 ,
,
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
【解析】(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值不大于2的整数有_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明身高为140cm,比他高20cm的哥哥的身高为_______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+25是完全平方式,那么k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成计算:
(1)先化简,再求值:(4ab3﹣8a2b2)÷4ab+(2a+b)(2a﹣b),其中a=2,b=1.
(2)因式分解:3x2﹣6axy+3ay2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
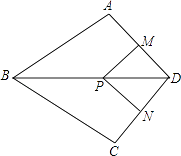
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数x、y分别满足|x|=5,y2=4,且xy<0,求x-y的值.
相关试题

