【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
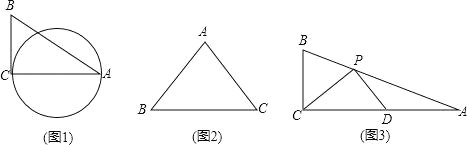
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
参考答案:
【答案】(1)2.(2)△ABC的伴随圆的半径分为![]() 或
或![]() 或
或![]() .(3)cos∠PDC=
.(3)cos∠PDC=![]() .
.
【解析】
试题分析:(1)先依据勾股定理求得AC的长,然后依据切线的性质可知AC为圆的直径,故此可求得△BAC的伴随圆的半径等于AC的一半;
(2)当O在BC上时,连接OD,过点A作AE⊥BC.由等腰三角形的性质和勾股定理求得AE=4,依据切线的性质可证明OD⊥AB,接下来证明△ODB∽△AEB,由相似三角形的性质可求得圆O的半径;当O在AB上且圆O与BC相切时,连接OD、过点A作AE⊥BC,垂足为E.先证明△BOD∽△BAE,由相似三角形的性质可求得圆O的半径,当O在AB上且圆O与AC相切时,连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.先依据面积法求得BF的长,然后再证明△AOD∽△ABF,由相似三角形的性质可求得圆O的半径;
(3)①连接OB、OP,先证明![]() ,从而得到PD∥OB,于是可得到∠1=∠4,接下来证明△BCO≌△BPO,从而可证明∠BPO=90°;②设圆O的半径为r,依据勾股定理定理依据求得PA、BC、OB的长,从而可求得cos∠1=
,从而得到PD∥OB,于是可得到∠1=∠4,接下来证明△BCO≌△BPO,从而可证明∠BPO=90°;②设圆O的半径为r,依据勾股定理定理依据求得PA、BC、OB的长,从而可求得cos∠1=![]() 接下来,由∠PDC=∠1可求得cos∠PDC=的值.
接下来,由∠PDC=∠1可求得cos∠PDC=的值.
试题解析:(1)∵∠C=90°,AB=5,BC=3,
∴AC=![]() =4.
=4.
∵BC是圆的切线,∠BCA=90°,
∴AC为圆的直径.
∴AC边上的半随圆的半径为2.
故答案为:2.
(2)当O在BC上时,如图(1)所示:连接OD,过点A作AE⊥BC.

∵AB=AC,AE⊥BC,
∴BE=EC=3.
在△AEB中,由勾股定理可知AE=![]() =4.
=4.
∵AB与⊙O相切,
∴OD⊥AB.
∴∠BDO=∠BEA=90°.
又∵∠OBD=∠EBA,
∴△ODB∽△AEB.
∴![]() .
.
设⊙O的半径为r.在OB=6﹣r.
∴![]() .
.
∴r=![]() .
.
∴△ABC的BC边上的伴随圆的半径为![]() .
.
当O在AB上时,如图(2),连接OD、过点A作AE⊥BC,垂足为E.

∵BC与⊙O相切,∴OD⊥BC.又∵AE⊥BC,
∴OD∥AE.∴△BOD∽△BAE.
∴![]() .
.
设⊙O的半径为r,则OB=5﹣r.∴![]() .∴r=
.∴r=![]() .
.
如图(3)所示:连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.

∵S△ABC=![]() BCAE=
BCAE=![]() ACBF,∴
ACBF,∴![]() ×6×4=
×6×4=![]() ×5×BF.∴BF=4.8.
×5×BF.∴BF=4.8.
∵AC与⊙O相切,∴DO⊥AC.∴DO∥BF.
∴△AOD∽△ABF.∴![]() 即
即![]() .∴r=
.∴r=![]() .
.
综上所述,△ABC的伴随圆的半径分为![]() 或
或![]() 或
或![]() .
.
(3)①证明:如图(4)连接OP、OB.

∵△CPD为直角三角形,
∴△CPD的外接圆圆心O在CD中点.
设⊙O的半径为r,则DC=2r,OA=3r.∴![]() .∵PA=2BP,
.∵PA=2BP,
∴![]() .∴
.∴![]() .∴PD∥OB.∴∠1=∠2,∠3=∠4.
.∴PD∥OB.∴∠1=∠2,∠3=∠4.
又∵∠3=∠2,∴∠1=∠4.在△BCO和△BPO中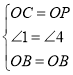 ,∴△BCO≌△BPO.
,∴△BCO≌△BPO.
∴∠BPO=∠BCO=90°.∴AB是圆O的切线.
∴△CPD的外接圆是△ABC某一条边上的伴随圆.
②如图(4)设圆O的半径为r.
∵在Rt△OAP中,OA=3r,OP=r,
∴PA=![]() =2
=2![]() r.
r.
∴AB=3![]() r.
r.
∵在Rt△ABC中,AC=4r,AB=3![]() r,
r,
∴BC=![]() =
=![]() a.
a.
∵在Rt△OBC中,OC=r,BC=![]() r,
r,
∴OB=![]() =
=![]() r.
r.
∴cos∠1=![]() =
=![]() =
=![]() .
.
∵∠PDC=∠1,
∴cos∠PDC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学要统计本校图书馆最受学生欢迎的图书种类,以下是打乱顺序的统计步骤:
①从扇形图中分析出最受学生欢迎的种类;
②去图书馆收集学生借阅图书的记录;
③绘制扇形图来表示各个种类所占的百分比;
④整理借阅图书记录并绘制频数分布表,正确统计步骤的顺序是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:
甲:作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;
乙:作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.
对于甲、乙两人的作法,下列判断何者正确( )
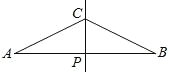
A. 两人都正确 B. 两人都错误 C. 甲正确,乙错误 D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法把3.1415926精确到千分位是_______;近似数3.0×106精确到______位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3(x+1)=9;
(2)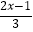 =1﹣
=1﹣ 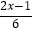 .
. -
科目: 来源: 题型:
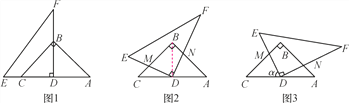
查看答案和解析>>【题目】(12分)如图1,已知Rt△ABC中,AB=BC,AC=2,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),点C在DE上,点B在DF上.
(1)求重叠部分△BCD的面积;
(2)如图2,将直角三角板DEF绕D点按顺时针方向旋转30度,DE交BC于点M,DF交AB于点N.
①求证:DM=DN;
②在此条件下重叠部分的面积会发生变化吗?若发生变化,请求出重叠部分的面积,若不发生变化,请说明理由;
(3)如图3,将直角三角板DEF绕D点按顺时针方向旋转α度(0<α<90),DE交BC于点M,DF交AB于点N,则DM=DN的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
相关试题

