【题目】如图,△ABC中,CD是边AB上的高,且![]() =
=![]() .
.
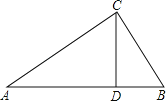
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
参考答案:
【答案】(1)见解析;(2)90°
【解析】
试题分析:(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;
(2)由(1)知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠BCD,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.
(1)证明:∵CD是边AB上的高,
∴∠ADC=∠CDB=90°,
∵![]() =
=![]() .
.
∴△ACD∽△CBD;
(2)解:∵△ACD∽△CBD,
∴∠A=∠BCD,
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
 x﹣2=4+
x﹣2=4+ x
x(2)
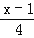 ﹣2=
﹣2=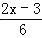
(3)
 [x﹣
[x﹣ (x﹣1)]=
(x﹣1)]=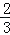 (x﹣
(x﹣ )
)(4)
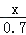 ﹣
﹣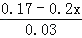 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果等腰三角形的两边长分别为2和5,则它的周长为( )
A. 9 B. 7 C. 12 D. 9或12
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3+2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
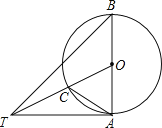
(1)求证:AT是⊙O的切线;
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )

A.甲公司近年的销售收入增长速度比乙公司快
B.乙公司近年的销售收入增长速度比甲公司快
C.甲、乙两公司近年的销售收入增长速度一样快
D.不能确定甲、乙两公司近年销售收入增长速度的快慢
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
②若第二列快车也从甲地出发匀速驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇后30分钟时,第二列快车与慢车相遇,直接写出第二列快车比第一列快车晚出发多少小时.
相关试题

