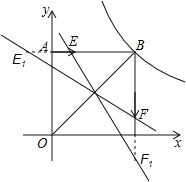
【题目】如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数![]() (x>0)图象上,△BOC的面积为8.
(x>0)图象上,△BOC的面积为8.

(1)求反比例函数![]() 的关系
的关系
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式?
(3)当运动时间为![]() 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() ;(2)S=-
;(2)S=-![]() +4;(3)P(
+4;(3)P(![]() ,0)
,0)
【解析】
试题分析:(1)设点B的坐标为(a,a),根据三角形的面积得出a的值,然后求出点B的坐标,计算反比例函数的解析式;(2)根据题意得出AE=t,BF=2t,BE=4-t,然后求出函数解析式;(3)根据对称轴得出点P的坐标.
试题解析:(1)∵四边形AOCB为正方形, ∴AB=BC=OC=OA,设点B坐标为(a,a),∵![]() C=8,
C=8,
∴![]() =8, ∴a=±4 又∵点B在第一象限,∴点B坐标为(4,4),
=8, ∴a=±4 又∵点B在第一象限,∴点B坐标为(4,4),
将点B(4,4)代入y=![]() 得,k=16 ∴反比例函数解析式为y=
得,k=16 ∴反比例函数解析式为y=![]()
(2)∵运动时间为t,∴AE=t,BF=2t ∵AB=4,∴BE=4-t,
∴![]() =
=![]() (4-t)2t=-
(4-t)2t=-![]() +4t=--
+4t=--![]() +4,
+4,
(3)存在.
当t=![]() 时,点E的坐标为(
时,点E的坐标为(![]() ,4),点F的坐标为(4,
,4),点F的坐标为(4,![]() )
)
作F点关于x轴的对称点![]() ,得F1(4,-
,得F1(4,-![]() ),经过点E、
),经过点E、![]() 作直线
作直线
由E(![]() ,4),
,4),![]() (4,-
(4,-![]() )代入y=ax+b得:
)代入y=ax+b得: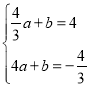 解得:
解得:
可得直线E![]() 的解析式是y=-2x+
的解析式是y=-2x+![]() 当y=0时,x=
当y=0时,x=![]() ∴P点的坐标为(
∴P点的坐标为(![]() ,0)
,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=5,BC=12,点A在⊙B上,如果⊙D与⊙B相交,且点B在⊙D内,那么⊙D的半径长可以等于 .(只需写出一个符合要求的数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
A. 9800名学生是总体 B. 每个学生是个体
C. 100名学生是所抽取的一个样本 D. 样本容量是100
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
(1)求证:EF∥AC;(2)求∠BEF大小;

-
科目: 来源: 题型:
查看答案和解析>>【题目】
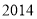 年
年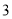 月
月 日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,我校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A级:90分——100分;B级:75分——89分;C级:60分——74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,我校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A级:90分——100分;B级:75分——89分;C级:60分——74分;D级:60分以下).请结合图中提供的信息,解答下列问题: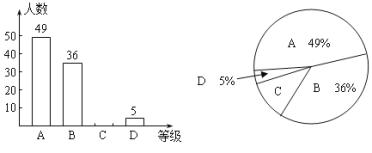
(1)扇形统计图中C级所在的扇形的圆心角度数是 .(2)请把条形统计图补充完整;
(3)若该校共有2000名学生,请你用此样本估计安全知识竞赛中A级和B级的学生共约有多少人?
-
科目: 来源: 题型:
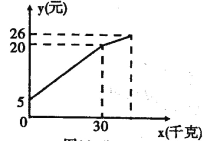
查看答案和解析>>【题目】一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,
结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a0+2b1﹣1=2b﹣1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组
 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
相关试题

