【题目】已知二次函数y=x2+bx+c的图象过点A(﹣3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是﹣2.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值.

参考答案:
【答案】(1)y=x2+2x﹣3;(2)![]()
【解析】试题分析: (1)把A(-3,0)和点B(1,0),代入y=x2+bx+c,建立关于b,c的二元一次方程组,求出b,c即可;
(2)先求出抛物线的对称轴,又因为A,B关于对称轴对称,所以连接BD与对称轴的交点即为所求P点.
试题解析:
(1)将A(-3,0),B(1,0)代入y=x2+bx+c,
得![]() ,解得
,解得![]()
∴y=x2+2x-3;
(2)∵y=x2+2x-3=(x+1)2-4
∴对称轴x=-1,
又∵A,B关于对称轴对称,
∴连接BD与对称轴的交点即为所求P点.
过D作DF⊥x轴于F将x=-2代入y=x2+2x-3,
则y=4-4-3=-3,
∴D(-2,-3)
∴DF=3, BF=1-(-2)=3
Rt△BDF中,BD=![]()
∵PA=PB,
∴PA+PD=BD=3![]()
故PA+PD的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
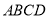 ,对角线
,对角线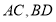 交于点
交于点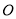 ,点
,点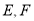 分别是
分别是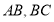 的中点,连接
的中点,连接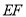 交
交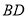 于
于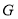 ,连接
,连接
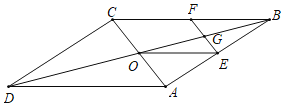
(1)证明:四边形
 是平行四边形
是平行四边形(2)点
 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)请直接写出点A关于原点O对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形
 中,
中, ,
, ,
, 是
是 上的一个动点,由
上的一个动点,由 向
向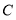 运动(与
运动(与 、
、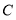 不重合),速度为每秒
不重合),速度为每秒 ,
, 是
是 延长线上一点,与点
延长线上一点,与点 以相同的速度由
以相同的速度由 向
向 延长线方向运动(不与
延长线方向运动(不与 重合),连结
重合),连结 交AB于
交AB于 .
.

(1)如图1,若
 ,
, ,求点P运动几秒后,
,求点P运动几秒后, .
.(2)在(1)的条件下,作
 于F,在运动过程中,线段
于F,在运动过程中,线段 长度是否发生变化,如果不变,求出
长度是否发生变化,如果不变,求出 的长;如果变化,请说明理由.
的长;如果变化,请说明理由.(3)如图3,当
 时,平行四边形的面积是
时,平行四边形的面积是 ,那么在运动中是否存在某一时刻,点P,Q关于点E成中心对称,若存在,求出a的值;若不存在,说明理由.
,那么在运动中是否存在某一时刻,点P,Q关于点E成中心对称,若存在,求出a的值;若不存在,说明理由. -
科目: 来源: 题型:
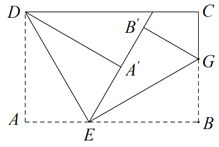
查看答案和解析>>【题目】如图,将长方形纸片的一角作折叠,使顶点 A 落在 A处, DE 为折痕,将 BEA对折,使得 B落在直线 EA上,得折痕 EG .
(1)求 DEG 的度数;
(2) 若 EA恰好平分 DEB ,求 DEA的度数 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为12 ,点B在点A右边,且OA2OB.
(1)写出数轴上点 B 表示的数;
(2)点 M 为数轴上一点,若 AM BM 4 ,求出点 M 表示的数.

相关试题

