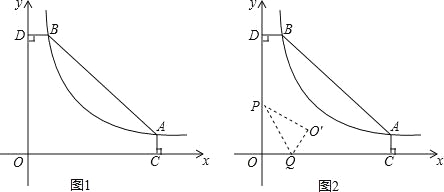
【题目】如图1,点A(8,1)、B(n,8)都在反比例函数y=![]() (x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.
(x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.
(1)求m的值和直线AB的函数关系式;
(2)动点P从O点出发,以每秒2个单位长度的速度沿折线OD﹣DB向B点运动,同时动点Q从O点出发,以每秒1个单位长度的速度沿折线OC向C点运动,当动点P运动到D时,点Q也停止运动,设运动的时间为t秒.
①设△OPQ的面积为S,写出S与t的函数关系式;
②如图2,当的P在线段OD上运动时,如果作△OPQ关于直线PQ的对称图形△O′PQ,是否存在某时刻t,使得点O′恰好落在反比例函数的图象上?若存在,求O′的坐标和t的值;若不存在,请说明理由.
参考答案:
【答案】(1)m=8,直线AB的解析式为y=﹣x+9;
(2)①S=![]() t×8=4t(4<t≤4.5);
t×8=4t(4<t≤4.5);
②存在,O′(4,2).
当t=![]() 个长度单位时,O′恰好落在反比例函数的图象上.
个长度单位时,O′恰好落在反比例函数的图象上.
【解析】
试题分析:(1)由于点A(8,1)、B(n,8)都在反比例函数y=![]() 的图象上,根据反比例函数的意义求出m,n,再由待定系数法求出直线AB的解析式;
的图象上,根据反比例函数的意义求出m,n,再由待定系数法求出直线AB的解析式;
(2)①由题意知:OP=2t,OQ=t,由三角形的面积公式可求出解析式;
②通过三角形相似,用t的代数式表示出O′的坐标,根据反比例函数的意义可求出t值.
试题解析:(1)∵点A(8,1)、B(n,8)都在反比例函数y=![]() 的图象上,
的图象上,
∴m=8×1=8,∴y=![]() ,∴8=
,∴8=![]() ,即n=1,
,即n=1,
设AB的解析式为y=kx+b,
把(8,1)、B(1,8)代入上式得:
![]() ,解得:
,解得:![]() .
.
∴直线AB的解析式为y=﹣x+9;
(2)①由题意知:OP=2t,OQ=t,
当P在OD上运动时,
S=![]() =t2(0<t≤4),
=t2(0<t≤4),
当P在DB上运动时,
S=![]() t×8=4t(4<t≤4.5);
t×8=4t(4<t≤4.5);
②存在,
当O′在反比例函数的图象上时,
作PE⊥y轴,O′F⊥x轴于F,交PE于E,
则∠E=90°,PO′=PO=2t,QO′=QO=t,
由题意知:∠PO′Q=∠POQ,∠QO′F=90°﹣∠PO′E,
∠EPO′=90′﹣∠PO′E,
∴△PEO′∽△O′FQ,
∴![]() ,
,
设QF=b,O′F=a,
则PE=OF=t+b,O′E=2t﹣a,
∴![]() ,
,
解得:a=![]() ,b=
,b=![]() ,
,
∴O′(![]() t,
t,![]() t),
t),
当O′在反比例函数的图象上时,
![]() ,
,
解得:t=±![]() ,
,
∵反比例函数的图形在第一象限,
∴t>0,∴t=![]() .∴O′(4,2).
.∴O′(4,2).
当t=![]() 个长度单位时,O′恰好落在反比例函数的图象上.
个长度单位时,O′恰好落在反比例函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:14,7,11,7,16,下列说法不正确的是( )
A. 平均数是11 B. 中位数是11 C. 众数是7 D. 极差是7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=
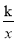 (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).

(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 ;
(2)写出点A1 , B1 , C1的坐标(直接写答案), A1________ ,B1________ ,C1________;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=
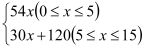
(1)李明第几天生产的粽子数量为420只?
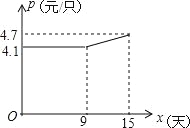
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图形来刻画.若李明第x天创造的利润为w元,求w关于x的函数表达式,并求出第几天的利润最大,最大利润时多少元?(利润=出厂价﹣成本)
相关试题

