【题目】计算题 ——
(1)用配方法解一元二次方程:2x2﹣4x﹣5=0.
(2)化简: ![]() ÷(x+2﹣
÷(x+2﹣ ![]() ).
).
参考答案:
【答案】
(1)解:2x2﹣4x﹣5=0,
x2﹣2x+1=1+ ![]() ,
,
(x﹣1)2= ![]() ,
,
x﹣1=± ![]() ,
,
x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]()
(2)解: ![]() ÷(x+2﹣
÷(x+2﹣ ![]() )
)
= ![]() ÷
÷ ![]()
= ![]() ×
× ![]()
= ![]()
【解析】(1)根据等式的性质:先把二次项的系数化为一,然后再在方程的两边加上一次项系数一半的平方,把左边配成完全平方式右边是一个非负常数,利用直接开平方法解出即可;
(2)把整式看成分母为一后通分进行分式的减法运算,然后再进行除法运算,运算的过程中分子分母能分解因式的分解因式,然后约分化为最简形式。
【考点精析】通过灵活运用分式的混合运算和配方法,掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=
 ∠B=
∠B= ∠C;
∠C;④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )

A.
B.2
C.3
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
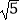 cm,且tan∠EFC=
cm,且tan∠EFC=  ,那么矩形ABCD的周长为cm.
,那么矩形ABCD的周长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
(1)如图1,在等腰三角形ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2.请用面积法证明:h1+h2=h;

(2)当点M在BC延长线上时,h1、h2、h之间的等量关系式是 ;(直接写出结论不必证明)
(3)如图2在平面直角坐标系中有两条直线l1:y=
 x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

相关试题

