【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF. 
(1)求证:EF是⊙O的切线;
(2)小强同学通过探究发现:AF+CF=2AO,请你帮助小强同学证明这一结论.
参考答案:
【答案】
(1)证明:连接OD,如图,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AF,
而AF⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
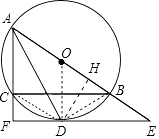
(2)证明:连接CD、BD,作DH⊥AB于H,如图,

∵AD平分∠BAC,DF⊥AF,DH⊥AB,
∴DF=DH,
在Rt△ADF和△ADH中
![]() ,
,
∴Rt△ADF≌△ADH,
∴AF=AH,
∵∠BAD=∠DAC,
∴ ![]() =
= ![]() ,
,
∴CD=BD,
在Rt△DCF和Rt△DBH中
![]() ,
,
∴Rt△DCF≌Rt△DBH,
∴CF=BH,
∴AF+CF=AH+BH=AB=2OA.
【解析】(1)连接OD,如图,利用平行线的判定证明OD∥AF,加上AF⊥EF,则OD⊥EF,于是根据切线的判定定理可判断EF是⊙O的切线;(2)连接CD、BD,作DH⊥AB于H,如图,先利用角平分线的性质得到DF=DH,再证明Rt△ADF≌△ADH得到AF=AH,证明Rt△DCF≌Rt△DBH得到CF=BH,所以AF+CF=AH+BH=AB=2OA.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半).
-
科目: 来源: 题型:
查看答案和解析>>【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+
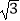 )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.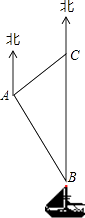
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=
 BC,②
BC,②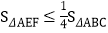 ,③
,③ AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
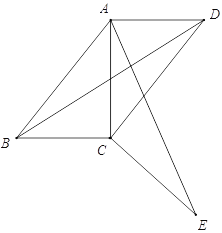
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)求证:AE⊥BD;
(2)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.
-
科目: 来源: 题型:
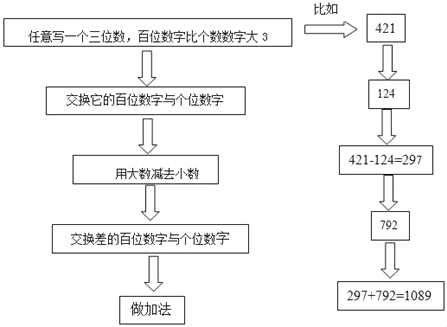
查看答案和解析>>【题目】按照下面的步骤计算:
任意写一个三位数,百位数字比个数数字大3交换差的百位数字与个位数字用大数减去小数交换它的百位数字与个位数字做加法
问题:(1)用不同的三位数再做两次,结果都是1089吗?
(2)你能解释其中的道理吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
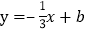 的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.(1)求b的值,并求出△PAB为等腰三角形时点P的坐标;
(2)在点P出发的同时,动点Q也从点A出发,以每秒
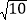 个单位的速度,沿射线AB运动,运动时间为t(s);
个单位的速度,沿射线AB运动,运动时间为t(s);①点Q的坐标(用含t的表达式表示);
②若点P的运动速度为每秒k个单位,请直接写出当△APQ为等腰三角形时k的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
相关试题

