【题目】如图,平面直角坐标系中,一次函数y=﹣2x+1的图象与y轴交于点A.
(1)若点A关于x轴的对称点B在一次函数y= ![]() x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
(2)求这两个一次函数的图象与y轴围成的三角形的面积.
参考答案:
【答案】
(1)解:∵把x=0代入y=﹣2x+1,得y=1.
∴点A坐标为(0,1),
∴点B坐标为(0,﹣1).
∵点B在一次函数y= ![]() x+b的图象上,
x+b的图象上,
∴﹣1= ![]() ×0+b,
×0+b,
∴b=﹣1.
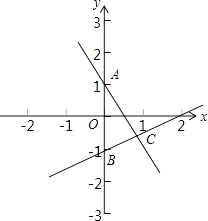
(2)解:设两个一次函数图象的交点为点C.
∵ 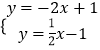 ,解得
,解得 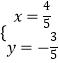 ,
,
∴点C坐标为( ![]() ,﹣
,﹣ ![]() ).
).
∴S△ABC= ![]() ×2×
×2× ![]() =
= ![]() .
.
【解析】(1)先求出A点坐标,再根据关于x轴对称的点的坐标特点得出B点坐标,代入一次函数y= ![]() x+b求出b的值即可得出其解析式,画出该函数图象即可;(2)设两个一次函数图象的交点为点C,联立两函数的解析式得出C点坐标,利用三角形的面积公式即可得出结论.
x+b求出b的值即可得出其解析式,画出该函数图象即可;(2)设两个一次函数图象的交点为点C,联立两函数的解析式得出C点坐标,利用三角形的面积公式即可得出结论.
【考点精析】关于本题考查的一次函数的图象和性质,需要了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.
-
科目: 来源: 题型:
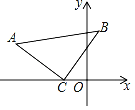
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解正确的是( )
A. x2﹣4=(x+4)(x﹣4) B. x2+x+1=(x+1)2
C. x2﹣2x﹣3=(x﹣1)2﹣4 D. 2x+4=2(x+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线y=k1x+b与x轴交于点B,与y轴交于点C,与反比例函数y=
 的图象在第一象限交于点A(3,1),连接OA.
的图象在第一象限交于点A(3,1),连接OA.(1)求反比例函数y=
 的解析式;
的解析式;(2)若S△AOB:S△BOC=1:2,求直线y=k1x+b的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.000 010 2=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,一点P(﹣2,3)关于原点的对称点P′的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2﹣3x+4与y轴的交点坐标是 .
相关试题

