【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
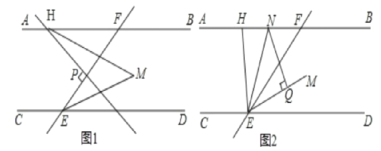
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
参考答案:
【答案】(1)45o (2)∠FHE=2∠ENQ或∠FHE=180°2∠ENQ,证明见解析
【解析】
(1)首先作MQ∥AB,根据平行线的性质,推得∠M=![]() (∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(2)①如图2,首先判断出∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
②如图3,首先判断出∠NEQ=∠QEF-∠NEF=![]() (∠DEF-∠HEF)=
(∠DEF-∠HEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
如图1,作MQ∥AB,
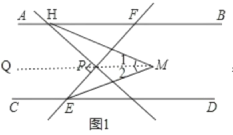
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=![]() (∠FHP+∠FED)=
(∠FHP+∠FED)= ![]() (∠FHP+∠HFP),
(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°90°=90°,
∵∠1+∠2=∠M,
∴∠M=![]() ×90°=45°.
×90°=45°.
(2)①如图2,

∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,

∠FHE=180°2∠ENQ,理由如下:
∠NEQ=∠QEF∠NEF=![]() (∠DEF∠HEF)=
(∠DEF∠HEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=180°∠CEH=180°2∠ENQ.
综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°2∠ENQ.
-
科目: 来源: 题型:
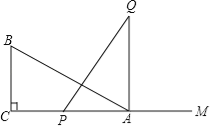
查看答案和解析>>【题目】如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

-
科目: 来源: 题型:
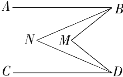
查看答案和解析>>【题目】如图,AB∥CD,BN,DN分别平分∠ABM,∠MDC,试问∠M与∠N之间的数量关系如何?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形AOCB的顶点A(m,n)和C(p,q)在坐标轴上,已知
 和
和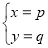 都是方程x+2y=4的整数解,点B在第一象限内.
都是方程x+2y=4的整数解,点B在第一象限内.(1)求点B的坐标;
(2)若点P从点A出发沿y轴负半轴方向以1个单位每秒的速度运动,同时点Q从点C出发,沿x轴负半轴方向以2个单位每秒的速度运动,问运动到多少秒时,四边形BPOQ面积为长方形ABCO面积的一半;
(3)如图2,将线段AC沿x轴正方向平移得到线段BD,点E(a,b)为线段BD上任意一点,试问a+2b的值是否变化?若变化,求其范围;若不变化,求其值.(直接写出结论)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克)
…
34.8
32
29.6
28
…
售价 x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于
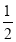 CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )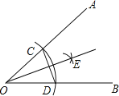
A.△OCD是等腰三角形B.CD垂直平分OE
C.点E到OA、OB的距离相等D.证明射线OE是角平分线的依据是SSS
相关试题

