【题目】甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.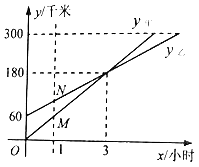
(1)直接写出y甲、y乙与x之间的函数表达式;
(2)如图,过点(1,0)作x轴的垂线,分别交y甲、y乙的图象于点M,N.求线段MN的长,并解释线段MN的实际意义;
(3)在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,求x的取值范围.
参考答案:
【答案】
(1)
解:设y甲=kx,
把(3,180)代入,得3k=180,解得k=60,
则y甲=60x;
设y乙=mx+n,
把(0,60),(3,180)代入,
得 ![]() ,解得
,解得 ![]() ,
,
则y乙=40x+60
(2)
解:当x=1时,
y甲=60x=60,y乙=40x+60=100,
则MN=100﹣60=40(千米),
线段MN的实际意义:表示甲、乙两人出发1小时后,他们相距40千米
(3)
解:分三种情况:
①当0<x≤3时,
(40x+60)﹣60x<30,解得x>1.5;
∴1.5<x≤3.
②当3<x≤5时,
60x﹣(40x+60)<30,解得x<4.5;
∴3<x≤4.5.
③当5<x≤6时,
300﹣(40x+60)<30,解得x>5.25.
∴5.25<x≤6.
综上所述,在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,x的取值范围是1.5<x<4.5或5.25<x≤6
【解析】(1)利用待定系数法即可求出y甲、y乙与x之间的函数表达式;
(2)把x=1代入(1)中的函数解析式,分别求出对应的y甲、y乙的值,则线段MN的长=y乙-y甲 , 进而解释线段MN的实际意义;
(3)分三种情况进行讨论:①0<x≤3;②3<x≤5;③5<x≤6.分别根据甲、乙两人距A地的路程差小于30千米列出不等式,解不等式即可.
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解某个年级的学习情况,在这个年级抽取了50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出表格:
分组]
50~59分
60~69分
70~79分
80~89分
90~99分
频率
0.04
0.04
0.16
0.34
0.42
(1)本次测试90分以上的人数有人;(包括90分)
(2)本次测试这50名学生成绩的及格率是;(60分以上为及格,包括60分)
(3)这个年级此学科的学习情况如何?请在下列三个选项中,选一个填在题后的横线上________.
A.好
B.一般
C.不好 -
科目: 来源: 题型:
查看答案和解析>>【题目】江涛同学统计了他家10月份的长途电话明细清单,按通话时间画出频数分布直方图.

(1)他家这个月一共打了 次长途电话;
(2)通话时间不足10分钟的 次;
(3)通话时间在分钟范围最多,通话时间在分钟范围最少. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果对顶角互补,那么两条直线互相________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解八年级学生的课外阅读情况,我校语文组从八年级随机抽取了若干名学生,对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图,请你依据图中提供的信息,解答下列问题:(每组含最小值不含最大值)
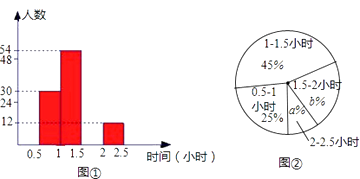
(1)从八年级抽取了多少名学生?
(2)填空(直接把答案填到横线上)
①“2-2.5小时”的部分对应的扇形圆心角为度;
②课外阅读时间的中位数落在(填时间段)内.
(3)如果八年级共有800名学生,请估算八年级学生课外阅读时间不少于1.5小时的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A. 120° B. 110° C. 100° D. 80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣x2+4x﹣3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是_____.
相关试题

