

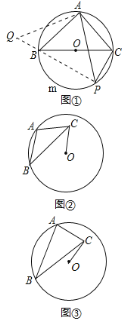
【题目】(1)问题背景:如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),求证:
上一动点(不与B,C重合),求证:![]() PA=PB+PC.请你根据图中所给的轴助线,给出作法并完成证明过程.
PA=PB+PC.请你根据图中所给的轴助线,给出作法并完成证明过程.
(2)类比迁移:如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值
(3)拓展延伸:如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为____________.
AC,AB⊥AC,垂足为A,则OC的最小值为____________.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将△ACP绕点A顺时针旋转90°到△ABQ的位置,由旋转的性质可得:∠QBA=∠PCA,AP=AQ,PC=QB,根据圆的内接四边形的性质可证点Q,点B,点P共线,根据勾股定理可证![]() AP=PQ=PC+PB;
AP=PQ=PC+PB;
(2)连接OA,将△OAC绕点A顺时针旋转90°至△EAB,连接OB,OE,则可得EB=OC,AE=OA=3,∠EAB=∠OAC,根据勾股定理可求OE=3![]() ,根据三角形三边关系可得BE≥OEOB=3
,根据三角形三边关系可得BE≥OEOB=3![]() 3(当点B在OE上时,取等号),即可求OC的最小值;
3(当点B在OE上时,取等号),即可求OC的最小值;
(3)如图③构造相似三角形即可解决问题,作AQ⊥OA,使得AQ=![]() OA,连接OQ,BQ,OB.由△QAB∽OAC,推出BQ=
OA,连接OQ,BQ,OB.由△QAB∽OAC,推出BQ=![]() OC,当BQ最小时,OC最小.
OC,当BQ最小时,OC最小.
解:(1)将△ACP绕点A顺时针旋转90°到△ABQ的位置,
∵BC是直径,
∴∠BAC=90°=∠BPC,
∵AB=AC,
∴∠ACB=∠ABC=45°,
由旋转可得∠QBA=∠PCA,PA=AQ,PC=QB,
∵∠PCA+∠PBA=180°,
∴∠QBA+∠PBA=180°,
∴Q,B,P三点共线,
∴∠QAB+∠BAP=∠BAP+∠PAC=90°
∴QP2=AP2+AQ2=2AP2,
∴QP=![]() AP=QB+BP=PC+PB,
AP=QB+BP=PC+PB,
∴![]() AP=PC+PB;
AP=PC+PB;
(2)如图②:连接OA,将△OAC绕点A顺时针旋转90°至△EAB,连接OB,OE,
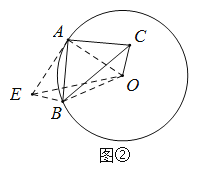
∵AB⊥AC,
∴∠BAC=90°,
由旋转可得:EB=OC,AE=OA=3,∠EAB=∠OAC,
∴∠EAB+∠BAO=∠BAO+∠OAC=90°,
∴在Rt△OAE中,OE=![]() =3
=3![]() ,
,
∵BE≥OEOB=3![]() 3(当点B在OE上时,取等号),
3(当点B在OE上时,取等号),
∴OC最小值是3![]() 3;
3;
(3)如图③中,作AQ⊥OA,使得AQ=![]() OA,连接OQ,BQ,OB,
OA,连接OQ,BQ,OB,

∵∠QAO=∠BAC=90°,∠QAB=∠OAC,
∵![]() ,
,
∴△QAB∽△OAC,
∴BQ=![]() OC,
OC,
当BQ最小时,OC最小,
易知OA=3,AQ=4,OQ=5,BQ≥OQOB,
∴BQ≥2,
∴BQ的最小值为2,
∴OC的最小值为![]() ,
,
故答案为:![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,CD是中线,
,CD是中线,![]() ,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F,DF与AE交于点M,DE与BC交于点N.
,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F,DF与AE交于点M,DE与BC交于点N.
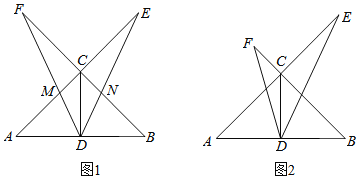
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,在![]() 绕点D旋转的过程中,试证明
绕点D旋转的过程中,试证明![]() 恒成立;
恒成立;
(3)若![]() ,
,![]() ,求DN的长.
,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:
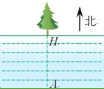
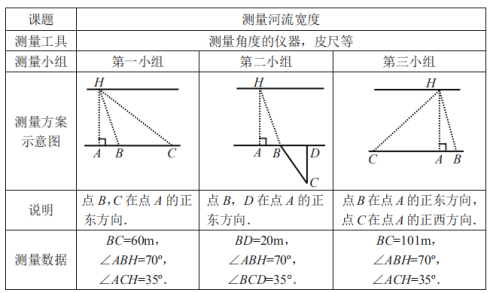
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到0.1m).
(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
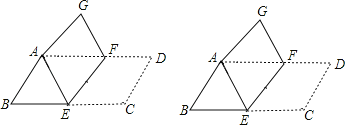
【题目】如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(1)连接CF,求证:四边形AECF是菱形;
(2)若E为BC中点,BC=26,tan∠B=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是切线,点
是切线,点![]() 为切点.
为切点.
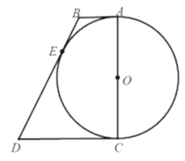
(1)求证:![]() ;
;
(2)如图,连接![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

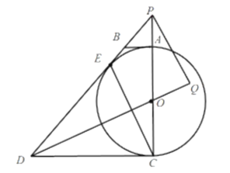
(3)如图,延长![]() 交于点
交于点![]() 连接
连接![]() 过点
过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]()
![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
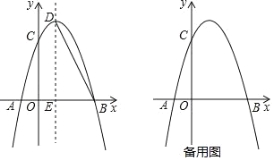
【题目】如图,抛物线y=-![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的表达式及对称轴;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com