【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用6天;③若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.试问:
(1)两队单独做各要几天完成?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理.
参考答案:
【答案】(1)甲,乙两队单独完成这项工程各需要6、12天(2)在不耽误工期的前提下,选第三种施工方案最节省工程款
【解析】试题分析:(1)关键描述语为:“甲,乙两队合做3天,余下的工程由乙队单独做也正好如期完成”;说明甲队实际工作了3天,乙队工作了x天完成任务,工作量=工作时间×工作效率,等量关系为:甲3天的工作量+乙规定日期的工作量=1,列方程求解.
(2)方案(1)、(3)不耽误工期,符合要求,可以求费用,方案(2)显然不符合要求.
解:(1)设规定日期为x天.由题意得
![]() +
+![]() +
+![]() =1
=1
3(x+6)+x2=x(x+6),
3x=18,解之得:x=6.经检验:x=6是原方程的根显然,
所以甲,乙两队单独完成这项工程各需要6、12天
(2)方案(2)不符合要求;
方案(1):1.2×6=7.2(万元);
方案(3):1.2×3+0.5×6=6.6(万元).
因为7.2>6.6,
所以在不耽误工期的前提下,选第三种施工方案最节省工程款
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:

解:因为AD∥BC(已知),
所以∠1=∠3( ).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥________( ).
所以∠3+∠4=180°( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
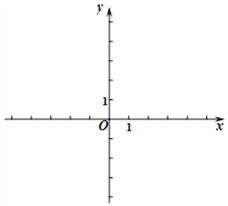
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示△ABC在边长为1个单位的网格中,请根据下列提示填空:
(1)为了把△ABC平移得到△A′B′C′,可以先将△ABC向 平移_______格,再向 平移_______格.
(2)求出△A’B’C’的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.

【答案】(1)60°.AD=BE;(2)AB=17;(3)∠AOE的度数是60°或120°.
【解析】试题分析:(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由(1)知△ACD≌△BCE,得∠CAD=∠CBE,由∠CAB=∠ABC=60°,可知∠EAB+∠ABE=120°,根据三角形的内角和定理可知∠AOE=60°.
试题解析:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
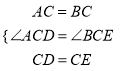 ,
,∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
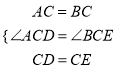 ,
,∴△ACD≌△BCE(SAS).
∴AD=BE=AE-DE=8,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC∠CED=90°.
∴AB=
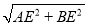 =17;
=17;(3)由(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°
∴∠AOE=180°120°=60°,
同理求得∠AOB=60°,
∴∠AOE=120°,
∴∠AOE的度数是60°或120°.
点睛:本题考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力.
【题型】解答题
【结束】
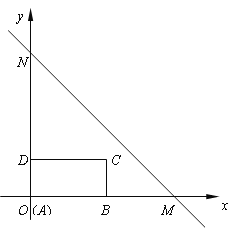
26【题目】如图,直线MN:y=-x+b与x轴交于点M(4,0),与y轴交于点N,长方形ABCD的边AB在x轴上,AB=2,AD=1.长方形ABCD由点A与点O重合的位置开始,以每秒1个单位长度的速度沿x轴正方向作匀速直线运动,当点A与点M重合时停止运动.设长方形运动的时间为t秒,长方形ABCD与△OMN重合部分的面积为S.
(1)求直线MN的解析式;
(2)当t=1时,请判断点C是否在直线MN上,并说明理由;
(3)请求出当t为何值时,点D在直线MN上;
(4)直接写出在整个运动过程中S与t的函数关系式
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 OAB与
OAB与 ODC是位似图形 。
ODC是位似图形 。 试问:(1)AB与CD平行吗?请说明理由 。
(2)如果OB=3,OC=4,OD=3.5.试求
 OAB与
OAB与 ODC的相似比及OA的长 。
ODC的相似比及OA的长 。
-
科目: 来源: 题型:
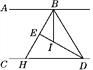
查看答案和解析>>【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
相关试题

