【题目】将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,求∠E1D1B的度数.

参考答案:
【答案】∠E1D1B=15°.
【解析】
试题分析:先根据已知条件得:△D1CE1各角的度数,由旋转得:∠BCE1=15°,证明△ABC≌△CBD1,可以得出结论.
试题解析:由题意得:∠CD1E1=∠D=30°,∠D1CE1=∠DCE=90°﹣30°=60°,
∵把△DCE绕点C顺时针旋转15°得到△D1CE1,∴∠BCE1=15°,
∴∠D1CB=60°﹣15°=45°,在△ACB和△CBD1中,
∵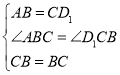 ,∴△ABC≌△CBD1,∴∠CD1B=∠A=45°,
,∴△ABC≌△CBD1,∴∠CD1B=∠A=45°,
∴∠E1D1B=∠CD1B﹣∠CD1E1=45°﹣30°=15°.
-
科目: 来源: 题型:
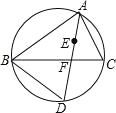
查看答案和解析>>【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D.
(1)求证:∠BAD=∠CBD;
(2)求证:DE=DB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学记数法表示为( )
A.0.7×10﹣3
B.7×10﹣3
C.7×10﹣4
D.7×10﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一问题中,自变量是( )
A.沙漠
B.体温
C.时间
D.骆驼 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为东明一中新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的位置坐标为B(-2,-1),解答以下问题:
(1)在图中找到坐标系中的原点,并建立直角坐标系;
(2)若体育馆的坐标为C(1,-3),食堂坐标为D(2,0),请在图中标出体育馆和食堂的位置;
(3)顺次连接教学楼、图书馆、体育馆、食堂得到四边形ABCD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4= .

-
科目: 来源: 题型:
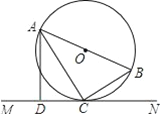
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=4,AC=5,求⊙O的直径.
相关试题

