【题目】如图,经过原点的抛物线![]() 与
与![]() 轴的另一个交点为A。过点P(1,m)作直线PM⊥
轴的另一个交点为A。过点P(1,m)作直线PM⊥![]() 轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B、点C不重合),连接CB,CP。
轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B、点C不重合),连接CB,CP。
⑴当![]() 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
⑵当![]() 时,连接CA,当CA⊥CP时,求
时,连接CA,当CA⊥CP时,求![]() 的值;
的值;
⑶过点P作PE⊥PC,且PE=PC,问是否存在m,使得点E恰好落在坐标轴上,若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由。

参考答案:
【答案】⑴A(5,0) BC=3;⑵![]() ⑶
⑶![]()
【解析】试题分析:(1)把m=![]() ,代入抛物线的解析式,令y=0解方程,得到的解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;
,代入抛物线的解析式,令y=0解方程,得到的解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;
(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△ACH∽△PCB,根据相似的性质得到:![]() ,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;
,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;
(3)存在,本题要分当m>1时,BC=2(m-1),PM=m,BP=m-1和当0<m<1时,BC=2(1-m),PM=m,BP=1-m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.
试题解析:(1)当m=![]() 时,y=-x2+5x;
时,y=-x2+5x;
令y=0,得-x2+5x=0.
∴x1=0,x2=5,
∴A(5,0).
当x=1时,y=4,
∴B(1,4).
∵抛物线y=-x2+5x的对称轴为直线x=![]() ,
,
又∵点B,C关于对称轴对称,
∴BC=3;
(2)过点C作CH⊥x轴于点H(如图).

由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB.
又∵∠AHC=∠PBC=90°,
tan∠ACH=tan∠PCB.
∴![]() .
.
∵抛物线y=-x2+2mx的对称轴为直线x=m,其中m>1,
又∵B,C关于对称轴对称,
∴BC=2(m-1).
∵B(1,2m-1),P(1,m),
∴BP=m-1.
又∵A(2m,0),C(2m-1,2m-1),
∴H(2m-1,0).
∴AH=1,CH=2m-1.
∴![]() ,
,
∴m=![]() ;
;
(3)存在.
∵B,C不重合,
∴m≠1,分两种情况:
①当m>1时,m=2,相对应的E点坐标是(2,0)或(0,4);
②当0<m<1时,m=![]() .,相对应的E点坐标是(
.,相对应的E点坐标是(![]() ,0);
,0);
∴E点坐标是(2,0)或(0,4)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为
 米.甲同学先步行
米.甲同学先步行 米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的
米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的
,公交车的速度是乙骑自行车速度的 倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到 分钟.根据以上信息回答:
分钟.根据以上信息回答:(
 )求乙骑自行车的速度.
)求乙骑自行车的速度.(
 )当甲到达学校时,乙同学离学校还有多远.
)当甲到达学校时,乙同学离学校还有多远. -
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式m2﹣4m+4分解因式的结果是_____.
-
科目: 来源: 题型:
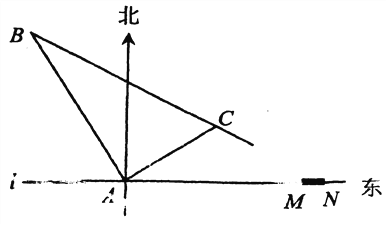
查看答案和解析>>【题目】在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得二架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5万千米的C处.
⑴该飞机航行的速度是多少千米/小时?(结果保留根号)
⑵如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程9x2﹣6x+k=0有两个不相等的实根,则k的范围是( )
A.k<1
B.k>1
C.k≤1
D.k≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】0是( )
A. 最小的自然数 B. 负数
C. 最小的整数 D. 既是正数,又是负数
相关试题

