【题目】如图,在平面直角坐标系中, ![]() 为坐标原点,点
为坐标原点,点![]() 在反比例函数
在反比例函数![]() 的图象上,作
的图象上,作![]() 轴于
轴于![]() 点.
点.
(1)![]() 的面积为______;
的面积为______;
(2)若点![]() 的横坐标为4,点
的横坐标为4,点![]() 在
在![]() 轴的正半轴,且
轴的正半轴,且![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标;
的坐标;
(3)动点![]() 从原点出发,沿
从原点出发,沿![]() 轴的正方向运动,以
轴的正方向运动,以![]() 为直角边,在
为直角边,在![]() 的右侧作等腰
的右侧作等腰![]() ,
, ![]() ;若在点
;若在点![]() 运动过程中,斜边
运动过程中,斜边![]() 始终在
始终在![]() 轴上,求
轴上,求 ![]() 的值.
的值.



参考答案:
【答案】6
【解析】分析: (1)首先过点B作BC⊥x轴于点C,由等腰三角形的三线合一,可得OC=AC=3,然后由顶点B在反比例函数![]() 的图象上,求得点B的坐标;
的图象上,求得点B的坐标;
(2)首先由等腰直角三角形的性质,可得OC=BC,然后由顶点B在反比例函数![]() 的图象上,求得点B的坐标,继而求得点A的坐标;
的图象上,求得点B的坐标,继而求得点A的坐标;
(3)首先过点P作PD⊥x轴于点D,易得AD=PD,则可设AD=b,则点P(4![]() +b,b),又由点P在反比例函数
+b,b),又由点P在反比例函数![]() 的图象上,求得b的值,继而求得答案.
的图象上,求得b的值,继而求得答案.
详解:
(1) 6
(2)依题意,得A(4,3),如图1,过A作AH⊥x轴于H,
∴AH=3,OH=4, ![]() ;
;
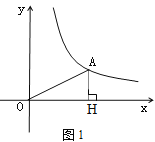
要使△OAP是等腰三角形,有如下三种情况:
①当OP=OA时,OP=5
∴点P的坐标为(5,0)
②当AO=AP时,OP=2OH=8
∴点P的坐标为(8,0)
③当PO=PA时,如图2,设点P的横坐标为![]() ,
,
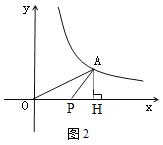
则PO=PA= ![]() ,PH=
,PH=![]()
在Rt△AHP中, ![]()
∴![]()
解得: ![]()
∴点P的坐标为(![]() ,0)
,0)
综上所述,点P的坐标为(5,0)或 (8,0) 或(![]() ,0)
,0)
(3)如图3,
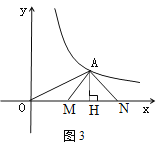
在等腰Rt△MAN,
∵AH⊥x轴于H
∴MH=AH=HN
∴ ON2-OM2=(ON+OM)(ON-OM)
=[(OH+HN)+(OH-MH)][(OH+HN)-(OH-MH)]
=(2OH)(HN+MH)
=(2OH)(2AH)
=4OH ![]() AH
AH
4x12 =48
点睛: 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中(请补画出必要的图形),
 为坐标原点,直线y=-2x+4与
为坐标原点,直线y=-2x+4与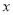 、
、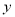 轴分别交于
轴分别交于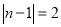 、
、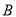 两点,过线段
两点,过线段 的中点
的中点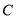 作
作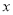 轴的垂线
轴的垂线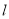 ,分别与直线
,分别与直线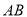 交于点
交于点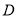 ,与直线y=x+n交于点
,与直线y=x+n交于点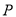 .
.(1)直接写出点A、B、C、
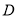 的坐标:A(____________),B(____________),C(_____________),D(____________);
的坐标:A(____________),B(____________),C(_____________),D(____________);
(2)若
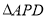 的面积等于1,求点P的坐标.
的面积等于1,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
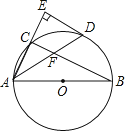
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据三视图求几何体的表面积.
下列各图是棱长为
 的小正方体摆成的,如图①中,共有
的小正方体摆成的,如图①中,共有 个小正方体,从正面看有
个小正方体,从正面看有 个正方形,表面积为
个正方形,表面积为 ;如图②中,共有
;如图②中,共有 个小正方体,从正面看有
个小正方体,从正面看有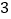 个正方形,表面积为
个正方形,表面积为 ;如图③,共有
;如图③,共有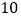 个小正方体,从正面看有
个小正方体,从正面看有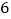 个正方形,表面积为
个正方形,表面积为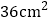 ;…
;… 第
第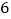 个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?
个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少? 第
第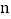 个图形中,从正面看有多少个正方形?表面积是多少?
个图形中,从正面看有多少个正方形?表面积是多少?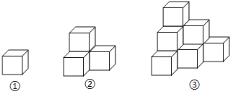
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:一粒米微不足道,平时在饭桌上总会毫不经意地掉下几粒,甚至有些挑食的同学把整碗米饭倒掉.针对这种浪费粮食现象,老师组织同学们进行了实际测算,称得
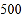 粒大米约重
粒大米约重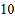 克.
克.尝试解决:
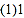 粒米重约多少克?
粒米重约多少克?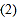 按我国现有人口
按我国现有人口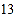 亿,每年
亿,每年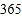 天,每人每天三餐计算,若每人每餐节约
天,每人每天三餐计算,若每人每餐节约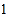 粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)
粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)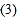 假设我们把一年节约的大米卖成钱,按每千克
假设我们把一年节约的大米卖成钱,按每千克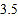 元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到
元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到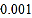 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
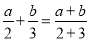 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: 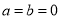 .我们称使得
.我们称使得 成立的一对数
成立的一对数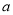 ,
, 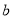 为“相伴数对”,记为
为“相伴数对”,记为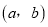 .
.(1)若
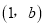 是“相伴数对”,求
是“相伴数对”,求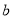 的值;
的值;(2)写出一个“相伴数对”
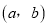 ,其中
,其中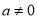 且
且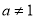 ;
;(3)若
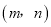 是“相伴数对”,求代数式
是“相伴数对”,求代数式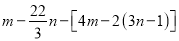 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时从点C出发,以1cm/s的速度分别沿CA、CB匀速运动.当点Q到达点B时,点P、Q同时停止运动.过点P作AC的垂线l交AB于点R,连接PQ、RQ,并作△PQR关于直线l对称的图形,得到△PQ′R.设点Q的运动时间为t(s),△PQ′R与△PAR重叠部分的面积为S(cm2).

(1)t为何值时,点Q′恰好落在AB上?
(2)求S与t的函数关系式,并写出t的取值范围;
(3)S能否为 cm2?若能,求出此时的t值;若不能,说明理由.
cm2?若能,求出此时的t值;若不能,说明理由.
相关试题

