【题目】如图,在正方形![]() 中,边长为
中,边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() 和
和![]() 上.
上.
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求![]() 的长;
的长;
(3)试求正方形![]() 的面积.
的面积.

参考答案:
【答案】(1)等腰直角三角形,证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由等边三角形和正方形的性质结合HL定理可证![]() ,从而求得BE=DF,然后求得CE=CF,从而可得△FCE的形状;
,从而求得BE=DF,然后求得CE=CF,从而可得△FCE的形状;
(2)在等腰直角三角形中,根据勾股定理求解即可;
(3)设BE=x,则AB=BC=![]() ,然后根据勾股定理列方程求解,从而求得AB的长,则正方形面积可求.
,然后根据勾股定理列方程求解,从而求得AB的长,则正方形面积可求.
解:(1)![]() 为等腰直角三角形
为等腰直角三角形
理由如下:![]() 是等边三角形
是等边三角形
所以![]() =
=![]() ,AE=AF=EF
,AE=AF=EF
又∵在正方形ABCD中,AB=AD
所以在![]() 和
和![]() 中
中![]()
∴![]()
∴BE=DF
∴CE=CF
∵∠C=90°,
∴![]() 为等腰直角三角形;
为等腰直角三角形;
(2)在等腰![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]()
解得:EC=![]() ;
;
(3)在![]() 中,
中,![]() ,
,
设BE=x,则AB=BC=![]() ,
,
根据勾股定理可得:![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
所以![]() ,
,![]() ,
,
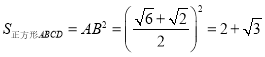 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的
 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用直接开平方法解方程:
(1) 4(x-2)2-36=0;
(2) x2+6x+9=25;
(3) 4(3x-1)2-9(3x+1)2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成相应的任务;全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时,我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形
 和四边形
和四边形 中,连接对角线
中,连接对角线 ,这样两个四边形全等的问题就转化为“
,这样两个四边形全等的问题就转化为“ ”与“
”与“ ”的问题。若先给定“
”的问题。若先给定“ ”的条件,只要再增加
”的条件,只要再增加 个条件使“
个条件使“ ”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。按照智慧小组的思路,小明对图
 中的四边形
中的四边形 与四边形
与四边形 先给出和下条件:
先给出和下条件:  ,
, ,小亮在此基础上又给出“
,小亮在此基础上又给出“ ”两个条件.他们认为满足这五个条件能得到“四边形
”两个条件.他们认为满足这五个条件能得到“四边形 四边形
四边形 ”.
”.
(1)请根据小明和小亮给出的条件,说明“四边形
 四边形
四边形 ”的理由;
”的理由;(2)请从下面
 两题中任选一题作答,我选择 题.
两题中任选一题作答,我选择 题. 在材料中“小明所给条件”的基础上,小颖又给出两个条件“
在材料中“小明所给条件”的基础上,小颖又给出两个条件“ ”.满足这五个条件 (填“能”或“不能”)得到四边形
”.满足这五个条件 (填“能”或“不能”)得到四边形 四边形
四边形
 在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形
在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形 四边形
四边形 ,你添加的条件是① ,② .
,你添加的条件是① ,② . -
科目: 来源: 题型:
查看答案和解析>>【题目】请认真观察图形,解答下列问题:
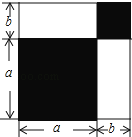
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm,如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足什么条件时,⊙P与直线CD相交?

相关试题

