【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
(1)如图①,若∠BAC=60°,按边分类:△CEF是 ____________ 三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;
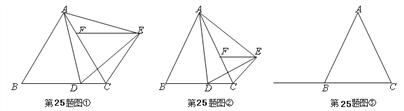
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形,写出结论并证明.
参考答案:
【答案】(1)等边;(2)①△BEF为等腰三角形,②△EFB为等腰三角形(3)等腰三角形
【解析】
试题(1)、根据题意推出△AED和△ABC为等边三角形,然后通过求证△EAF≌△DAC,结合平行线的性质,即可推出△EFC为等边三角形;(2)、①根据(1)、的推理依据,即可推出△EFC为等腰三角形;②根据题意画出图形,然后根据平行线的性质,通过求证△EAF≌△DAC,推出等量关系,即可推出△CEF为等腰三角形.
试题解析:(1)、等边;
(2)、①△CEF为等腰三角形,
理由如下:∵AB=AC,AD=AE,∠BAC=∠DAE,∴△AED和△ABC为等腰三角形,
∴∠ACB=∠ABC,∠EAD=∠CAE,∴△EAC≌△BAD,∴∠ABC=∠ACE,∵EF∥BC,
∴∠EFC=∠ACB,∵在△EFB中,∠EFC=∠ACE, ∴△EFB为等腰三角形,
②AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.
∵△BEF为等腰三角形,∵AB=AC,AD=AE,∠BAC=∠DAE,
∴△AED和△ABC为等腰三角形, ∴∠ACB=∠ABC,∠EAB=∠DAC,
∴△EAF≌△DAC, ∴∠EBA=∠ACD, ∴∠EBF=∠ACB,
∵EF∥BC, ∴∠AFE=∠ABC, ∵∠ABC=∠ACB, ∴∠AFE=∠ACB,
∵在△EFB中,∠EBF=∠AFE, ∴△EFB为等腰三角形.
(3)、等腰三角形.
-
科目: 来源: 题型:
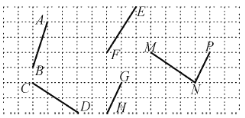
查看答案和解析>>【题目】如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:__________,__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意有理数x、y定义运算如下:x△y=ax+by+cxy,这里a、b、c是给定的数,等式右边是通常数的加法及乘法运算,如当a=1,b=2,c=3时,l△3=1×l+2×3+3×1×3=16,现已知所定义的新运算满足条件,1△2=3,2△3=4,并且有一个不为零的数d使得对任意有理数x△d=x,求a、b、c、d的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简.
(1)( x- y)( x+ y) ( x2+ y2) ( x4+ y4)·…·(x16+ y16);
(2)(22+1)(24+1)(28+1)(216+1).
-
科目: 来源: 题型:
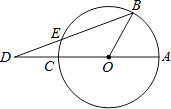
查看答案和解析>>【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
A.DE=EB
B.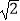 DE=EB
DE=EB
C.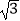 DE=DO
DE=DO
D.DE=OB -
科目: 来源: 题型:
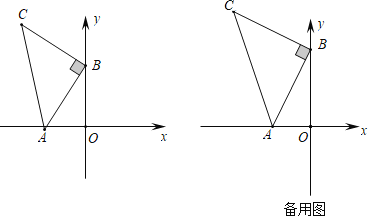
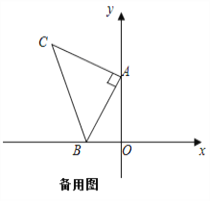
查看答案和解析>>【题目】如图,平面直角坐标系中有点B(﹣1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=2时,在坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.
相关试题

