【题目】△ABC中,AB=AC,AC边上的中线BD把.△ABC的周长分成12、15两部分,则BC=_____.
参考答案:
【答案】11或7
【解析】
由题意可知有两种情况,AB+AD=12或AB+AD=15,从而根据等腰三角形的性质及三角形三边关系即可求出底边.
如图所示:
∵BD是等腰△ABC的中线,可设AD=CD=x,则AB=AC=2x,
又知BD将三角形周长分为12和15两部分,
∴可知分为两种情况
AB+AD=12,即3x=12,解得x=4,此时BC=15-x=15-4=11,故三边为8,8,11,成立;
AB+AD=15,即3x=15,解得x=5;此时BC=12-x=12-5=7,故三边为10,10,7,成立;
∴这个三角形的底边长为11或7.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,……,若∠A1=α,则∠A2019为( )
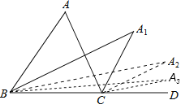
A.
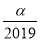 B.
B. 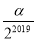 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:
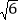 ≈2.449,结果保留整数)
≈2.449,结果保留整数)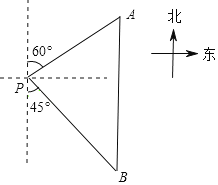
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证:BC平分∠DBE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
16
戏剧
4
散文
a
其他
b
合计
1
根据图表提供的信息,解答下列问题:
(1)直接写出a,b,m的值;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用列表法或画树状图的方法,求选取的2人恰好乙和丙的概率.

-
科目: 来源: 题型:
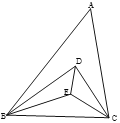
查看答案和解析>>【题目】如图,△ABC中,∠A=57°,BD、BE将∠ABC三等分,CD、CE将∠ACB三等分,则∠BDE=_______.
相关试题

