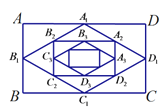
【题目】如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为(______).
参考答案:
【答案】5
【解析】根据菱形和矩形的性质以及三角形中位线的性质以及勾股定理求出四边形各边长得出规律求出即可.
解:∵矩形ABCD中,AB=6,AD=8,顺次连结矩形形ABCD各边中点,
∴四边形A1B1C1D1是菱形,
∴A1B1=5,
∴四边形A1B1C1D1的周长是:5×4=20,
同理可得出:A2D2=8×![]() =4,C2D2=
=4,C2D2=![]() AB=
AB=![]() ×6=3,
×6=3,
∴A3D3=![]() ,
,
∴四边形A3B3C3D3的周长是:![]() ×4=10,
×4=10,
…
∴四边形A5B5C5D5周长是:![]() ×
×![]() ×4=5.
×4=5.
故答案为:5.
“点睛”此题主要考查了菱形的性质以及矩形的性质和中点四边形的性质等知识,根据已知得出边长变化规律是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
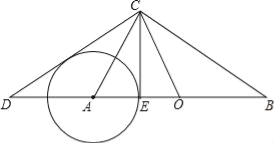
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=
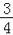 ,BC=10,求CE的长;
,BC=10,求CE的长;(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月31日,昌平区举办了首届初二年级学生“数学古文化阅读展示”活动,为表彰在本次活动中表现优秀的学生,老师决定在6月1日购买笔袋或彩色铅笔作为奖品. 已知1个笔袋、2筒彩色铅笔原价共需44元;2个笔袋、3筒彩色铅笔原价共需73元.
(1)每个笔袋、每筒彩色铅笔原价各多少元?
(2)时逢“儿童节”,商店举行“优惠促销”活动,具体办法如下:笔袋“九折”优惠;彩色铅笔不超过10筒不优惠,超出10筒的部分“八折”优惠. 若买x个笔袋需要y1元,买x筒彩色铅笔需要y2元. 请用含x的代数式表示y1、y2;
(3)若在(2)的条件下购买同一种奖品95件,请你分析买哪种奖品省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=2x2﹣4x+3的图象绕原点旋转180°后得到的图象的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
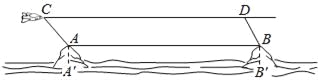
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3x2﹣6xy+3y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据5,2,3,5,4,5的众数是( )
A. 3B. 4C. 5D. 8
相关试题

