搜索
【题目】如图，△ABC中，D、E分别为AB、AC的中点，则△ADE与△ABC的面积比为 ． 
参考答案：
【答案】1：4
【解析】解：∵D、E分别为AB、AC的中点，
∴DE= 
BC，DE∥BC，
∴△ADE∽△ABC，
∴ 
=（ 
）2= 
，
所以答案是：1：4．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
（1）请直接写出线段AF，AE的数量关系；
（2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；
（3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】（3分）如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40cm，24cm，则AB= cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+bx+c与x轴交于点A，点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．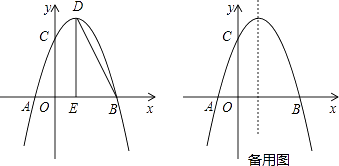
（1）求抛物线的解析式及点D的坐标；
（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；
（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在平面内，以线段MN为对角线作正方形MPNQ，请直接写出点Q的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O是△ABC的内切圆，若∠ABC=70°，∠ACB=40°，则∠BOC=°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为2，点E，F分别在边AD，CD上，若∠EBF=45°，则△EDF的周长等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请仔细观察图中等边三角形图形的变化规律，写出你发现关于等边三角形内一点到三边距离的数学事实：_____________________
相关试题
