【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

参考答案:
【答案】9n+3
【解析】
试题分析:∵第1个图由1个正六边形、6个正方形和6个等边三角形组成,
∴正方形和等边三角形的和=6+6=12=9+3;
∵第2个图由11个正方形和10个等边三角形组成,
∴正方形和等边三角形的和=11+10=21=9×2+3;
∵第3个图由16个正方形和14个等边三角形组成,
∴正方形和等边三角形的和=16+14=30=9×3+3,
…,
∴第n个图中正方形和等边三角形的个数之和=9n+3.
故答案为:9n+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
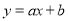 与反比例函数
与反比例函数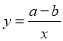 ,其中
,其中 ,
,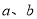 为常数,它们在同一坐标系中的图象可以是( ).
为常数,它们在同一坐标系中的图象可以是( ).A.
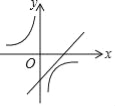 B.
B.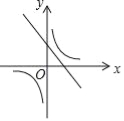 C.
C.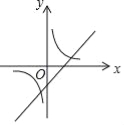 D.
D.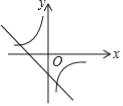
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一个多边形的某顶点出发,连接其余各顶点,把该多边形分成了5个三角形,则这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸片
 的边
的边 斜着向
斜着向 边对折,使点
边对折,使点 落在
落在 上,记为
上,记为 ,折痕为
,折痕为 ;再将
;再将 边斜向下对折,使点
边斜向下对折,使点 落在
落在 上,记为
上,记为 ,折痕为
,折痕为 ,
, ,
, .则矩形纸片
.则矩形纸片 的面积为 .
的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
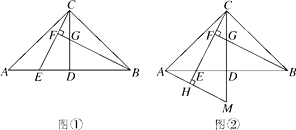
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为____.
相关试题

