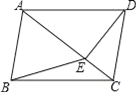
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
参考答案:
【答案】(1)证明见解析;(2)S平行四边形ABCD =3![]() .
.
【解析】试题分析:(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;
(2)证明△ABE是等边三角形,得出AE=AB=2,由直角三角形的性质求出CE和DE,得出AC的长,即可求出四边形ABCD的面积.
试题解析:(1)∵AB∥CD,∴∠ABC+∠DCB=180°,
∵∠ABC=∠ADC,∴∠ADC+∠BCD=180°,∴AD∥BC,
∵AB∥CD,∴四边形ABCD是平行四边形;
(2)∵sin∠ACD=![]() ,∴∠ACD=60°,
,∴∠ACD=60°,
∵四边形ABCD是平行四边形,∴AB∥CD,CD=AB=2,∴∠BAC=∠ACD=60°,
∵AB=BE=2,∴△ABE是等边三角形,∴AE=AB=2,
∵DE⊥AC,∴∠CDE=90°﹣60°=30°,∴CE=![]() CD=1,∴DE=
CD=1,∴DE=![]() CE=
CE=![]() ,AC=AE+CE=3,
,AC=AE+CE=3,
∴S平行四边形ABCD =2S△ACD =ACDE=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在正方形ABCD中,AB=1,
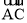 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作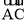 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点.(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
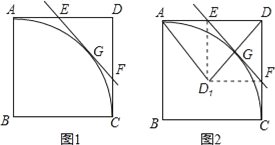
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1,D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2,﹣2),B(﹣1,﹣2),则直线AB与x轴的位置关系是( )
A.相交
B.平行
C.相互垂直
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3,5)到x轴的距离有个单位长度,到y轴的距离有个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
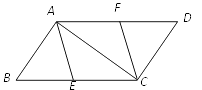
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式2a2-4b-1的值为3,则a2-2b的值是______.
相关试题

