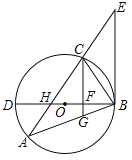
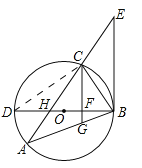
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.
(2)由△ABC∽△CBG,得![]() 求出BC,再由△BFC∽△BCD,得
求出BC,再由△BFC∽△BCD,得![]() =BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
=BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
试题解析:(1)连接CD,∵BD是直径,∴∠BCD=90°,即∠D+∠CBD=90°,∵∠A=∠D,∠A=∠EBC,∴∠CBD+∠EBC=90°,∴BE⊥BD,∴BE是⊙O切线.
(2)∵CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,∵∠CBG=∠ABC
∴△ABC∽△CBG,∴![]() ,即
,即![]() =BGBA=48,∴BC=
=BGBA=48,∴BC=![]() ,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴
,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴![]() =BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=
=BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=![]() =
=![]() ,∴CG=CF+FG=
,∴CG=CF+FG=![]() ,在RT△BFG中,BG=
,在RT△BFG中,BG=![]() =
=![]() ,∵BGBA=48,∴BA=
,∵BGBA=48,∴BA=![]() ,即AG=
,即AG=![]() ,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=
,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=![]() ,∵△ABC∽△CBG,∴
,∵△ABC∽△CBG,∴![]() ,∴AC=
,∴AC=![]() =
=![]() ,∴AH=AC﹣CH=
,∴AH=AC﹣CH=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线
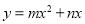 相交于A(1,
相交于A(1,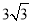 ),B(4,0)两点.
),B(4,0)两点.(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出
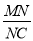 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.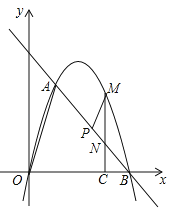
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:2(a+1)﹣a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.
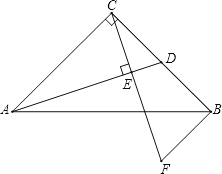
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数值中不是不等式5x≥2x+9的解的是( )
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线
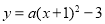 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,
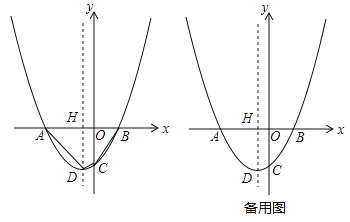
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,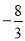 ),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.
),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.(1)求a的值及点A,B的坐标;
(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;
(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1或5 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为

A. 2 B. 3 C. 2或3 D. 1或5
相关试题

