Question

【题目】(2016·新疆中考)如图，在⊙O中，半径OA⊥OB，过OA的中点C作FD∥OB交⊙O于D、F两点，且CD＝，以O为圆心，OC为半径作弧CE，交OB于E点．

(1)求⊙O的半径OA的长；

(2)计算阴影部分的面积．

Answer 1

【答案】（1）2 （2）

解：(1)连接OD.∵OA⊥OB，∴∠AOB＝90°.∵CD∥OB，∴∠OCD＝90°.在Rt△OCD中，∵C是AO的中点，CD＝，∴OD＝2OC.设OC＝x，∴x2＋()2＝(2x)2，∴x＝1，∴OD＝2，∴⊙O的半径为2；

(2)∵sin∠CDO＝＝，∴∠CDO＝30°.∵FD∥OB，∴∠DOB＝∠CDO＝30°，∴S阴影＝S△CDO＋S扇形OBD－S扇形OCE＝×1×＋－＝＋.

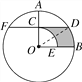
【解析】试题分析：（1）连接OD，首先根据平行线的性质证明OA⊥DF，设OC＝x，则OD＝2x，在Rt△OCD中利用勾股定理列方程即可解决问题；

（2）由OD＝2CO推出∠CDO＝30°，由平行线的性质得出∠DOB＝30°，根据S阴＝S△CDO＋S扇形OBD－S扇形OCE计算即可．

试题解析：解：（1）连接OD．

∵OA⊥OB，

∴∠AOB＝90°．

∵CD∥OB，

∴∠OCD＝90°．

在Rt△OCD中，∵C是AO的中点，CD＝，

∴OD＝2OC．

设OC＝x，

∴x2＋()2＝(2x)2，

∴x＝1，

∴OD＝2，

∴⊙O的半径为2；

（2）∵sin∠CDO＝＝，

∴∠CDO＝30°．

∵FD∥OB，

∴∠DOB＝∠CDO＝30°，

∴S阴影＝S△CDO＋S扇形OBD－S扇形OCE

＝×1×＋－

＝＋．