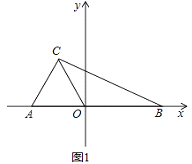
【题目】在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2)(见图1),且 ![]()
(1)求a、b的值;
(2)①在x轴的正半轴上存在一点M,使三角形COM的面积是三角形ABC的面积的一半,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使三角形COM的面积三角形ABC的面积的一半仍然成立? 若存在,请直接写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时, ![]() 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.

参考答案:
【答案】(1)a=-2,b=3;(2)满足条件的点M坐标为(2.5,0)或(-2.5,0)或(0,5)或(0,-5);(3)![]() =2,理由见解析.
=2,理由见解析.
【解析】试题分析:
(1)由![]() 列出关于a、b的方程组,即可解得a、b的值;
列出关于a、b的方程组,即可解得a、b的值;
(2)①由题意设点M的坐标为(x,0),在OM=![]() ,结合△COM的面积是△ABC面积的一半,列出方程,解方程结合点M在x轴的正半轴即可求得此时点M的坐标;
,结合△COM的面积是△ABC面积的一半,列出方程,解方程结合点M在x轴的正半轴即可求得此时点M的坐标;
②由①中的结果可得点M在x轴负半轴时的坐标;当M在y轴上时,可设点M的坐标为(0,y),结合△COM的面积是△ABC面积的一半,列出方程,解方程即可求得点M在y轴上的符合条件的坐标;
(3)由题意易证∠OPD=∠POB=2∠BOF,∠DOE+∠DOF=90°,∠BOF+∠DOF=90°,由此可得到∠OPD=2∠BOF=2∠DOE,从而可得![]() =2.
=2.
试题解析:
(1)∵![]() ,
,
∴![]() ,解得
,解得![]() ;
;
(2)①由(1)中结论可知点A、B的坐标分别为(-2,0)和(3,0),
∴AB=5,
又∵点C的坐标为(-1,2),
∴S△ABC=![]() ,
,
当点M在x轴上时,设点M的坐标为(x,0),则OM=![]() ,由题意可得:
,由题意可得:
![]() ,解得
,解得![]() ,
,
∵点M在x轴的正半轴,
∴点M的坐标为(2.5,0);
②由①中结论可知当点M在x轴的负半轴时,点M的坐标为(-2.5,0);
当点M在y轴上时,如下图,可设点M的坐标为(0,y),则OM=![]() ,由题意可得:
,由题意可得:
![]() ,解得:
,解得: ![]() ,
,
∴此时点M的坐标为(0,5)或(0,-5);
综上所述,当点M在坐标轴上时,其坐标分别为(2.5,0)、(-2.5,0)、(0,5)和(0,-5);
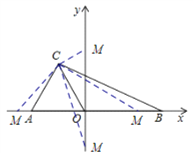
(3)如图2,∵CD⊥y轴,
∴CD∥OB,
∴∠OPD=∠POB,
∵OF平分∠POB,
∴∠OPD=∠POB=2∠BOF,
∵OE⊥OF,
∴∠EOF=∠DOB=90°,
∴∠DOE+∠DOF=∠DOF+∠BOF=90°,
∴∠DOE=∠BOF,
∴∠POD=2∠DOE,
∴![]() =2.
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为______.(n≥2,且n为整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个系数为负数,含有x、y的五次单项式,如_____.
-
科目: 来源: 题型:
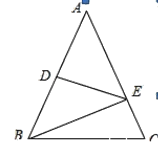
查看答案和解析>>【题目】如图,已知AB=AC,DE垂直平分AB交AC、AB于E、D两点,若AB=12cm,BC=10cm,∠A=50°,求△BCE的周长和∠EBC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国人很早就开始使用负数,中国古代数学著作《九章算术》.如果收入120元记作+120元,那么-100元表示( )
A.支出20元B.支出100元C.收入20元D.收入100元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设
 =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
相关试题

