【题目】已知∠AOB=108°,∠BOC=22°,射线OD、OE分别是∠AOB和∠BOC的平分线,求∠DOE的度数.
参考答案:
【答案】∠DOE的度数为43°或65°.
【解析】
分两种情况讨论:(1)当OC在∠AOB的内部时;(2)当OC在∠AOB的外部时,分别作出图形,利用角平分线的定义进行角度计算.
(1)当OC在∠AOB的内部时,如图1所示:
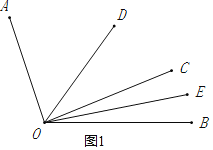
∵OE是∠BOC的平分线,
∴∠BOE=∠COE=![]() ∠BOC,
∠BOC,
又∵∠BOC=22°,
∴∠COE=11°,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD=![]() ∠AOB,
∠AOB,
又∵∠AOB=108°,
∴∠BOD=54°,
又∵∠BOC+∠COD=∠BOD,
∵∠COD=54°﹣22°=32°,
又∵∠DOE=∠DOC+COE,
∴∠DOE=32°+11°=43°;
(2)当OC在∠AOB的外部时,如图2所示:
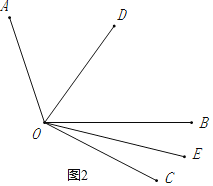
∵OE是∠BOC的平分线,
∴∠BOE=∠COE=![]() ∠BOC,
∠BOC,
又∵∠BOC=22°,
∴∠BOE=11°,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD=![]() ∠AOB,
∠AOB,
又∵∠AOB=108°,
∴∠BOD=54°,
又∵∠DOE=∠BOD+∠BOE,
∴∠DOE=54°+11°=65°;
综合所述,∠DOE的度数为43°或65°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在A,B两地分别有同型号的机器17台和15台,目前需要把这些机器中的18台运往甲地,14台运往乙地.从A,B两地运往甲,乙两地的费用如表:
甲地(元/台)
乙地(元/台)
A地
600
500
B地
400
800
(1)设从A地运往甲地x台,则从A地运往乙地 台,从B地运往乙地 台.(结果用x的代数式表示,且代数式化到最简)
(2)当运送总费用为15800元时,请确定运送方案(即A,B两地运往甲、乙两地的机器各几台).
(3)能否有一种运送方案比(2)中方案的总运费低?如果有,直接写出运送方案及所需运费;如果没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,在平面直角坐标系中如图所示:完成下列问题:

(1)画出△ABC绕点O逆时针旋转90后的△A
 B
B C
C ;点B1的坐标为___;
;点B1的坐标为___;(2)在(1)的旋转过程中,点B运动的路径长是___
(3)作出△ABC关于原点O对称的△A
 B
B C
C ;点C
;点C 的坐标为___.
的坐标为___. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α<∠β,下列表达式:①90°﹣∠α;②∠β﹣90°;③
 (∠β+∠α);④
(∠β+∠α);④ (∠β﹣∠α)中,等于∠α的余角的式子有( )
(∠β﹣∠α)中,等于∠α的余角的式子有( )A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题。
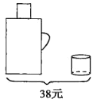
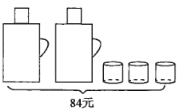
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1,3,5,7,9,…,排列成如图所示的数表:
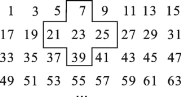
(1)十字框中的五个数的和与中间数23有什么关系?
(2)设中间数为
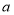 ,用式子表示十字框中五个数之和.
,用式子表示十字框中五个数之和.(3)将十字框上、下、左、右平移,可框住另外五个数,这五个数还有这种规律吗?
(4)十字框中的五个数之和能等于2015吗?若能,请写出这五个数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①
 ②
②
③
 ④
④
⑤
 ⑥
⑥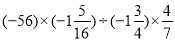
⑦
 ⑧
⑧
相关试题

