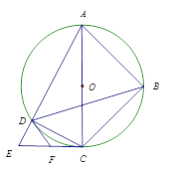
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=a, ![]() ∶DE=4∶1,写出求DE长的思路.
∶DE=4∶1,写出求DE长的思路.
参考答案:
【答案】(1)证明见解析;(2)答案见解析
【解析】试题解析:(1)连接OD,由AC为圆O的直径,得∠ADC为直角,从而ΔCDE为直角,再由点F为CE的中点,得∠FDC=∠FCD,再由OD=OC得∠ODC=∠OCD,由∠FCD+∠OCD=90°得∠FDC+∠ODC=90°, 即DF是⊙O的切线;
(2)![]() 由DB平分∠ADC,AC为⊙O的直径,证明△ABC是等腰直角三角形;
由DB平分∠ADC,AC为⊙O的直径,证明△ABC是等腰直角三角形;![]() 由AB=a,求出AC的长度为
由AB=a,求出AC的长度为![]() ;
;![]() 由∠ACE=∠ADC=90°,∠CAE是公共角,证明△ACD∽△AEC,得到
由∠ACE=∠ADC=90°,∠CAE是公共角,证明△ACD∽△AEC,得到![]() ;
;![]() 设DE为x,由
设DE为x,由![]() ∶DE=4∶1,求出
∶DE=4∶1,求出![]() .
.
试题解析:(1)证明:连接OD.
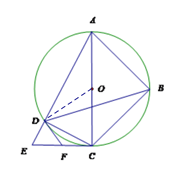
∵ OD=CD,
∴ ∠ODC=∠OCD.
∵ AC为⊙O的直径,
∴ ∠ADC=∠EDC=90°.
∵ 点F为CE的中点,
∴ DF=CF.
∴ ∠FDC=∠FCD.
∴ ∠FDO=∠FCO.
又∵ AC⊥CE,
∴ ∠FDO=∠FCO=90°.
∴ DF是⊙O的切线.
(2)①由DB平分∠ADC,AC为⊙O的直径,证明△ABC是等腰直角三角形;
②AB=a,求出AC的长度为![]() ;
;
③由∠ACE=∠ADC=90°,∠CAE是公共角,证明△ACD∽△AEC,得到![]() ;
;
④设DE为x,由![]() ∶DE=4∶1,求出
∶DE=4∶1,求出![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )

A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )
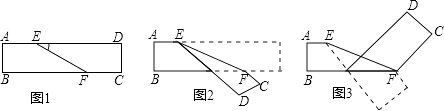
A.160°
B.150°
C.120°
D.110° -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)
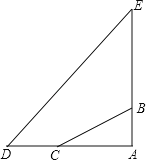
-
科目: 来源: 题型:
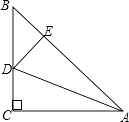
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )cm.
A.6
B.8
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣y=7,xy=2,则x2+y2的值为( )
A.53
B.45
C.47
D.51 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( ).
A.等弧对等弦;B.在同圆中,相等的弦所对的圆周角相等;
C.平分弦的直径垂直于弦;D.经过切点的直线是圆的切线.
相关试题

