【题目】如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.
(1)求此抛物线的表达式;
(2)假如这条抛物线与x轴交于点A,B,与y轴交于点C,已知点A在点B左侧,试判断△OCB的形状.

参考答案:
【答案】(1)抛物线的表达式为y=x2-2x-3;(2)△OCB是等腰直角三角形.
【解析】试题分析:(1)待定系数法求解可得;
(2)分别求出抛物线与坐标轴的交点即可得出答案.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,
将(﹣2,5),(0,﹣3)和(1,﹣4)三点代入,
得: 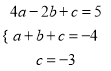 ,
,
解得: 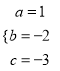 ,
,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)令y=0,即x2﹣2x﹣3=0,
解得:x=﹣1或x=3,
∴抛物线与x轴的两个交点为(﹣1,0)、(3,0),
∵c=﹣3,
∴抛物线与y轴的交点为(0,﹣3),
∴OB=OC,
∴△OCB是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
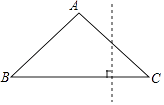
A.110°
B.115°
C.120°
D.125° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数:0,32,(-5)2,-4,-|-16|,π,其中有平方根的个数是( )
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“五一”节的到来,某食品连锁店对某种商品进行了跟踪调查,发现每天它的销售价与销售量之间有如下关系:
每千克售价(元)
25
24
23
…
15
每天销售量(千克)
30
32
34
…
50
如果单价从最高25元/千克下调到x元/千克时,销售量为y千克,已知y与x之间的函数关系是一次函数:
(1)求y与x之间的函数解析式;(不写定义域)
(2)若该种商品成本价是15元/千克,为使“五一”节这天该商品的销售总利润是200元,那么这一天每千克的销售价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:
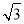 ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,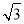 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某文具店,一支铅笔的售价为1.2元,一支圆珠笔的售价为2元,该店在新年之际举行文具优惠销售活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.设该铅笔卖出x支,则可得的一元一次方程为( )
A.0.8×1.2x+0.9×2(60﹣x)=87
B.0.8×1.2x+0.9×2(60+x)=87
C.0.9×2x+0.8×1.2(60+x)=87
D.0.9×2x+0.8×1.2(60﹣x)=87
相关试题

