搜索
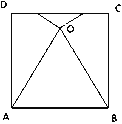
【题目】如图，将正方形ABCD的边AD和边BC折叠，使点C与点D重合于正方形内部一点O，已知点O到边CD的距离为a，则点O到边AB的距离为 .（用a的代数式表示）
参考答案：
【答案】（3+2
）a.
【解析】
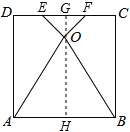
试题分析：本题考查的是翻转变换的性质和等边三角形的性质，翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．作OG⊥CD于G，交AB于H，根据翻转变换的性质得到OA=AD，OB=BC，∠EOA=∠D=90°，∠FOB=∠C=90°，根据直角三角形的性质和勾股定理求出DE、EF、FC，得到正方形的边长，计算即可．
作OG⊥CD于G，交AB于H，
∵CD∥AB，
∴OH⊥AB于H，
由翻转变换的性质可知，OA=AD，OB=BC，∠EOA=∠D=90°，∠FOB=∠C=90°，
∴△OAB是等边三角形，∠EOF=120°，
∴∠OEF=30°，
∴EO=2a，EG=a，
∴DE=OE=2a，OF=FC=2a，EF=2EG=2a，
∴DC=4a+2a，
∴点O到边AB的距离为4a+2a-a=3a+2a=（3+2）a．
故答案为（3+2）a．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算正确的是( )
A. (ab)2＝ab2 B. 3a＋2a2＝5a3 C. (a＋b)2＝a2＋b2 D. －(2a2)2·a＝－4a5
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆锥的底面半径为3cm，母线长为5cm，则圆锥的侧面积是（ ）
A. 20cm2 B. 20πcm2 C. 15cm2 D. 15πcm2
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明：
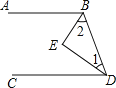
已知：如图．BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°．求证：AB∥CD．
证明：∵DE平分∠BDC（已知），
∴∠BDC=2∠1（_______________）．
∵BE平分∠ABD（已知），
∴∠ABD=2∠2（_____________）．
∴∠BDC+∠ABD=2∠1+2∠2=2（∠1+∠2）（__________）．
∵∠1+∠2=90°（已知），
∴∠ABD+∠BDC=______（__________）．
∴AB∥CD（______________）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】据悉，合肥轨道交通1号线、2号线建设总投资253.7亿元，其中253.7亿用科学记数法表示为_______________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若正比例函数的图像经过(1，-2)，则这个图像必经过点( )
A.(-1，-2)B.(-1，2)C.(2，-1)D.(-2，-1)
-
科目： 来源： 题型：
查看答案和解析>>【题目】将以此函数y=2x-1的图像向上平移2个单位长度后，得到的直线解析式为( )
A.y=2x+2B.y=2x+1C.y=2x+3D.y=2x-5
相关试题
