Question

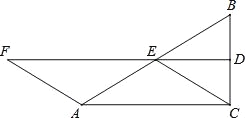
【题目】如图，△ABC中，∠ACB=90°，D、E分别是BC、BA的中点，连接DE，F在DE延长线上，且AF=AE．

（1）求证：四边形ACEF是平行四边形；

（2）若四边形ACEF是菱形，求∠B的度数．

Answer 1

【答案】（1）证明参见解析；（2）30°．

【解析】

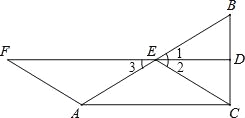
试题分析：（1）如下图：根据直角三角形斜边上的中线等于斜边的一半可得CE=AE=BE，从而得到AF=CE，再根据等腰三角形三线合一的性质可得∠1=∠2，根据等边对等角可得∠F=∠3，因为∠1=∠3，即可求出∠2=∠F，再根据同位角相等，两直线平行求出CE∥AF，然后利用一组对边平行且相等的四边形是平行四边形求证；（2）根据菱形的四条边都相等可得AC=CE，然后求出AC=CE=AE，从而得到△AEC是等边三角形，再根据等边三角形的每一个角都是60°求出∠CAE=60°，然后根据直角三角形两锐角互余解答．

试题解析：（1）∵∠ACB=90°，E是BA的中点，直角三角形斜边上的中线等于斜边的一半，∴CE=AE=BE，∵AF=AE，∴AF=CE，在△BEC中，∵BE=CE且D是BC的中点，∴ED是等腰△BEC底边上的中线，∴ED也是等腰△BEC的顶角平分线，∴∠1=∠2，∵AF=AE，∴∠F=∠3，∵∠1=∠3，∴∠2=∠F，∴CE∥AF，又∵CE=AF，∴四边形ACEF是平行四边形（一组对边平行且相等的四边形是平行四边形）；（2）∵四边形ACEF是菱形，∴AC=CE，由（1）知，AE=CE，∴AC=CE=AE，∴△AEC是等边三角形，∴∠CAE=60°，在Rt△ABC中，∠B=90°﹣∠CAE=90°﹣60°=30°．故∠B=30°．