【题目】一个四边形的边长依次是a,b,c,d,且a2+b2+c2+d2=2ac+2bd,则这个四边形是______,依据是________.
参考答案:
【答案】 平行四边形 两组对边分别相等的四边形是平行四边形
【解析】解:a2+b2+c2+d2=2ac+2bd,(a2﹣2ac+c2)+(b2﹣2bd+d2)=0,(a﹣c)2+(b﹣d)2=0,∴a﹣c=0,b﹣d=0,∴a=c,b=d,∴四边形是平行四边形(两组对边分别相等的四边形是平行四边形).故答案为:平行四边形,两组对边分别相等的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AB=2 BC=4,点E、F分别是BC、AD的中点.
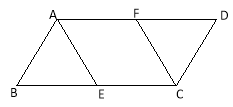
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有四个点A,B,C,D,过其中每两个点画直线可以画出直线的条数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
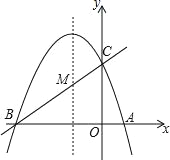
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2x-3(2x-3)=x+4;
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.1:2
B.2:1
C.1:4
D.4:1
相关试题

