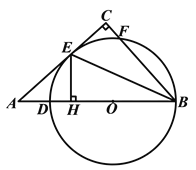
【题目】如图,在△![]() 中,∠
中,∠![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 相切于点
相切于点![]() ,与边
,与边![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)连接OE.由切线的性质得到OE⊥AC,从而有OE∥BC,由平行线的性质得到∠OEB=∠CBE.再由等腰三角形的性质得到∠OEB=∠OBE,即有∠OBE=∠CBE,由角平分线的性质即可得出结论;
(2)解Rt△ABC得到AB的长.再由OE∥BC,得到△AEO∽△ACB,由相似三角形对应边成比例,得到OB的长,进而可得出结论.
详解:(1)连接OE.
∵⊙O与边AC相切,∴OE⊥AC.
∵∠C=90°,∴OE∥BC,∴∠OEB=∠CBE.
∵OB=OE,∴∠OEB=∠OBE,∴∠OBE=∠CBE.
∵EH⊥AB,∴EH=EC.
(2)在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ∥
∥![]() ,∴△AEO∽△ACB,
,∴△AEO∽△ACB,
∴![]() ,即
,即![]() .
.
解得:![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
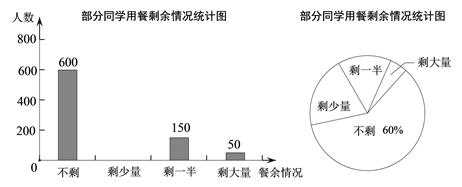
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市为加快美丽乡村建设,建设秀美幸福宿州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)乙镇3个A类美丽村庄和6个B类村庄改建共需资金多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,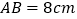 ,点
,点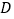 是
是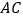 边的中点,点
边的中点,点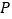 是边
是边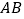 上的一个动点,过点
上的一个动点,过点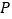 作射线
作射线 的垂线,垂足为点
的垂线,垂足为点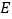 ,连接
,连接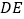 .设
.设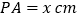 ,
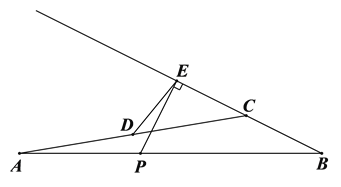
,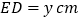 .
.
小石根据学习函数的经验,对函数
 随自变量
随自变量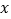 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了
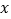 与
与 的几组值,如下表:
的几组值,如下表: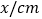
0
1
2
3
4
5
6
7
8
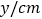
3.0
2.4
1.9
1.8
2.1
3.4
4.2
5.0
(说明:补全表格时相关数据保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
点
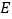 是
是 边的中点时,
边的中点时,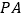 的长度约为
的长度约为 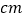 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
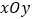 中,抛物线
中,抛物线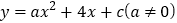 经过点
经过点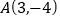 和
和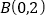 .
.(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线
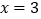 翻折,得到图象N.若过点
翻折,得到图象N.若过点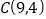 的直线
的直线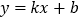 与图象M、图象N都相交,且只有两个交点,求b的取值范围.
与图象M、图象N都相交,且只有两个交点,求b的取值范围. -
科目: 来源: 题型:
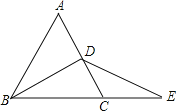
查看答案和解析>>【题目】已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,求DE的长.
相关试题

