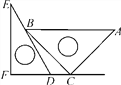
【题目】一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12![]() ,试求CD的长.
,试求CD的长.
参考答案:
【答案】CD=12-4![]() .
.
【解析】试题分析:过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=60°,求得MD的长,进而求得CD的长.
试题解析:
过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=45°,AC=![]() ,
,
∴BC=AC=![]() ,∠ABC=45°,
,∠ABC=45°,
∵AB∥CF,
∴∠BCM=∠ABC=45°,
∴BM=BC·sin45°=12,CM=BM=12,
∴在△EFD中,∠F=90°,∠E=30°,
∴∠EDF=60°.
∴MD=BM÷tan60°= ![]() ,
,
∴CD=CM-MD=12-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
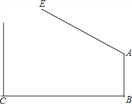
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
-
科目: 来源: 题型:
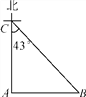
查看答案和解析>>【题目】如图,海面上B,C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A,B两岛之间的距离.(结果精确到0.1海里)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.

(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:
 ≈1.7)
≈1.7)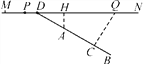
-
科目: 来源: 题型:
查看答案和解析>>【题目】请认真阅读,回答下面问题:如图,
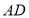 为
为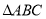 的中线,
的中线,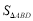 与
与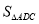 相等吗?(友情提示:
相等吗?(友情提示: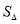 表示三角形面积)
表示三角形面积)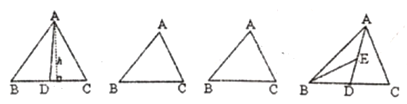
解:过
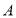 点作
点作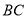 边上的高
边上的高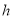 ,
,∵
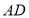 为
为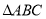 的中线
的中线∴
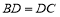
∵
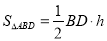
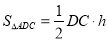
∴
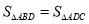
(1)用一句简洁的文字表示上面这段内容的结论;
(2)利用上面所得的结论,用不同的割法分别把下面两个三角形面积4等分,(只要割线不同就算一种)
(3)已知:
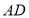 为
为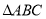 的中线,点
的中线,点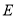 为
为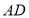 边上的中点,若
边上的中点,若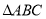 的面积为20,
的面积为20,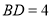 ,求点
,求点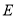 到
到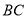 边的距离为多少?
边的距离为多少?
相关试题

