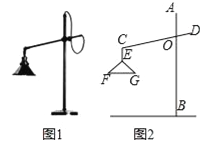
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
参考答案:
【答案】(1)130°;(2)13.6cm.
【解析】
试题分析:(1)由EF=EG可知∠G=∠F=40°,由三角形的内角和为180°可求出∠FEG的大小,根据已知条件可得知∠CEF=∠CEG,由∠CEF+∠FEG+∠GEC为周角可得出结论;
(2)延长FG交AB于点N,过点E作EM⊥AB于点M,延长CE交FG于点H,找出四边形CHNM为长方形,在Rt△CMO中由三角函数值求出CM的长度,再结合点G到OB的距离为12cm可求出HG的长度,由△EFG为等腰三角形可得知FG=2HG,从而得出结论.
试题解析:(1)∵EF=EG,∠F=40°,∴∠G=40°,∠FEG=180°﹣∠F﹣∠G=100°,∵灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,∴∠CEG=∠CEF=![]() =130°.
=130°.
(2)延长FG交AB于点N,过点E作EM⊥AB于点M,延长CE交FG于点H,如图所示.
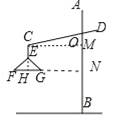
∵CE∥AB,FG处于水平位置,EM⊥AB,∴四边形CHNM为长方形,CH⊥FG,∴CM=HN.
在Rt△OMC中,OC=20cm,∠COM=70°,∠OMC=90°,∴CM=OCsin∠COM≈20×0.940=18.8(cm),∵GN=12cm,HN=CM,∴HG=CM﹣GN=6.8(cm).
∵EF=EG,CH⊥FG,∴FH=HG=![]() FG,∴FG=2×6.8=13.6(cm).
FG,∴FG=2×6.8=13.6(cm).
答:灯罩的宽度为13.6cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AB=10,则△BDE的周长等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果α是锐角,且tanα=cot20°,那么α=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车队运送一批货物,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,不仅装完全部货物,并且其中有一辆车只装了3.5吨。这个汽车队共派了多少辆汽车运输这批货物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )
A.1<AB<2
B.2<AB<10
C.4<AB<10
D.4<AB<20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=
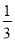 AC;
AC;(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于
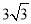 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.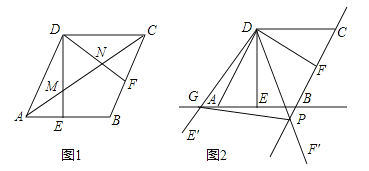
相关试题

