【题目】如图,在直角坐标系中,点A(-2,0),B(4,0),现同时将点A、B分别向上平移4个单位,再向右平移2个单位,得到点A、B的对应点C、D,连接AC,CD、BD.
(1)直接写出点C、D的坐标,求四边形ABDC的面积;
(2)动点P从点C出发,以每秒1个单位的速度,沿射线CO运动.设点P运动时间为t秒.连结PA,设三角形AOP的面积为S ,求S与t之间的关系式;
(3)如图,在(2)的条件下,在线段BO上取一点E,使2BE=OB,连接PB、CE相交于点F,当三角形AOP的面积是四边形ABDC的![]() 时,求点F的坐标.
时,求点F的坐标.

参考答案:
【答案】(1)(1)C(0,4)D(6,4)![]() =24;(2)见解析;(3)F(
=24;(2)见解析;(3)F(![]() ,
,![]() )
)
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可,再根据平行四边形的面积公式列式计算即可得解;
(2)分点P在点O上方时求出OP的长度,然后再表示三角形AOP的面积;点P在点O下方时,求出OP的长,然后再表示三角形AOP的面积;
(3)求出点P、E的坐标,然后利用待定系数法求出直线CE、BP的解析式,联立求出点F的坐标即可得解.
解:(1)∵点A(-2,0),B(4,0)分别向上平移4个单位,再向右平移2个单位,
∴点C、D的坐标分别为(0,4),(6,4),
S四边形ABDC=6×4=24;
(2)①点P在点O上方时,OP=4-t,OA=2,
∴S=4-t,
②点P在点O下方时,OP=t-4,OA=2,
∴S=t-4;
(3)当三角形AOP的面积是四边形ABDC的![]() 时,
时,
4-t=![]() ×24 ,
×24 ,
解得t=1,
∴P(0,3),
∵2BE=OB,
∴E(2,0),
易求直线CE的解析式为y=-2x+4,
直线BG的解析式为y=-![]() x+3,
x+3,
联立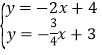 ,
,
解得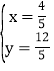 ,
,
∴点F 的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
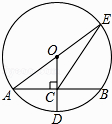
A.2
B.8
C.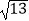
D.2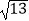
-
科目: 来源: 题型:
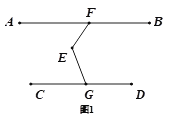
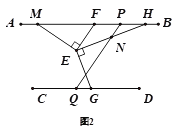
查看答案和解析>>【题目】已知:F、G分别为直线AB、CD上的点,E为平面内任意一点,连接EF、EG,∠AFE+∠CGE=∠FEG.
(1)如图(1),求证:AB∥CD,
(2)如图(2),过点E作EM⊥EF、EH⊥EG交直线AB上的点M、H,点N在EH上,过N作PQ∥EF.求证∶∠HNQ=∠MEG.
(3)如图(3)在(2)的条件下,若∠ENQ=∠EMF,∠EGD=110°,求∠CQP的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在双曲线y=
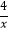 上,点B在双曲线y=
上,点B在双曲线y= 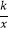 (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 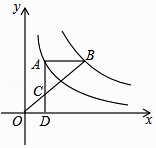
A.6
B.9
C.10
D.12 -
科目: 来源: 题型:
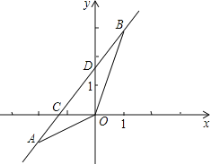
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,且DE是△ABC的中位线.延长ED到F,使DF=ED,连接FC,FB.回答下列问题:
(1)试说明四边形BECF是菱形.
(2)当
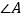 的大小满足什么条件时,菱形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,菱形BECF是正方形?请回答并证明你的结论.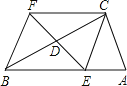
-
科目: 来源: 题型:
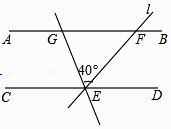
查看答案和解析>>【题目】如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=70°,那么∠GFE=度.
相关试题

