【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣6,0),B(﹣1,1),C(﹣3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1 . 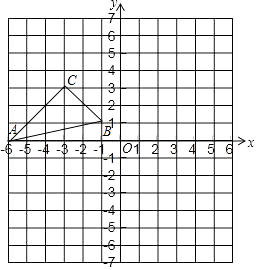
(1)画出△A1BC1 , 写出点A1、C1的坐标;
(2)计算线段BA扫过的面积.
参考答案:
【答案】
(1)解:如图,△A1BC1,A1(﹣2,6),C1(1,3);

(2)解:BA= ![]() =
= ![]() ,
,
所以线段BA扫过的面积= ![]() =
= ![]() π
π
【解析】(1)利用网格特点和旋转的性质画出点A、C的对应点A1、C1 , 从而得到△A1BC1;(2)先计算出BA的长,然后根据弧长公式求解.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
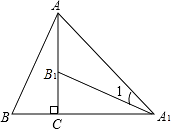
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1 , 若∠AA1B1=15°,则∠B的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2x2﹣x=1
(2)x2+4x+2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为
 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P.
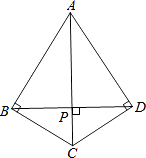
(1)请作出Rt△ABC的外接圆⊙O;(保留作图痕迹,不写作法)
(2)点D在⊙O上吗?说明理由;
(3)试说明:AC平分∠BAD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数与反比例函数y=
 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)点P是x轴上的一动点,试确定点P使PA+PB最小,并求出点P的坐标.
相关试题

