【题目】射线OA、OB、OC、OD、OE有公共端点O.
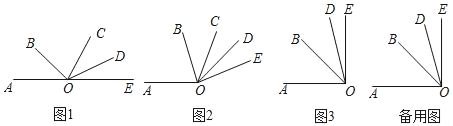
(1)若OA与OE在同一直线上(如图1),试写出图中小于平角的角;
(2)若∠AOC=108°,∠COE=n°(0<n<72),OB平分∠AOE,OD平分∠COE(如图2),求∠BOD的度数;
(3)如图3,若∠AOE=88°,∠BOD=30°,射OC绕点O在∠AOD内部旋转(不与OA、OD重合).探求:射线OC从OA转到OD的过程中,图中所有锐角的和的情况,并说明理由.
参考答案:
【答案】(1)图1中小于平角的角∠AOD,∠AOC,∠AOB,∠BOE,∠BOD,∠BOC,∠COE,∠COD,∠DOE;(2)∠BOD=54°;(3)∠AOE+∠AOB+∠AOC+∠AOD+∠BOC+∠BOD+∠BOE+∠COD+∠COE+∠DOE=412°.理由见解析.
【解析】
(1)根据角的定义即可解决;
(2)利用角平分线的性质即可得出∠BOD=![]() ∠AOC+
∠AOC+![]() ∠COE,进而求出即可;
∠COE,进而求出即可;
(3)将图中所有锐角求和即可求得所有锐角的和与∠AOE、∠BOD和∠BOD的关系,即可解题.
(1)如图1中小于平角的角∠AOD,∠AOC,∠AOB,∠BOE,∠BOD,∠BOC,∠COE,∠COD,∠DOE.

(2)如图2,

∵OB平分∠AOE,OD平分∠COE,∠AOC=108°,∠COE=n°(0<n<72),
∴∠BOD=![]() ∠AOD﹣
∠AOD﹣![]() ∠COE+
∠COE+![]() ∠COE=
∠COE=![]() ×108°=54°;
×108°=54°;
(3)如图3,

∠AOE=88°,∠BOD=30°,
图中所有锐角和为∠AOE+∠AOB+∠AOC+∠AOD+∠BOC+∠BOD+∠BOE+∠COD+∠COE+∠DOE
=4∠AOB+4∠DOE=6∠BOC+6∠COD
=4(∠AOE﹣∠BOD)+6∠BOD
=412°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
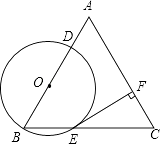
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是( )
A. 形状相同 B. 周长相等 C. 面积相等 D. 全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】新农村建设前,某乡在一条笔直的公路旁依次有A、B、D、E、F五个村庄(每相邻两个村庄之间有农田).后来由于新农村建设需要,在该公路旁新建了C庄,已知C庄在A庄和F庄之间,B庄是A庄和C庄的中点,E庄是C庄和F庄的中点,D庄是B庄和E庄的中点.
(1)按题意画出大致示意图;
(2)若A庄和C庄相距4千米,C庄和F庄相距12千米,求C庄和D庄之间的距离;
(3)若A庄和F庄之间的距离是C庄和D庄之间距离的8倍,求A庄和C庄之间的距离与C庄和F庄之间的距离的比值是多少?
-
科目: 来源: 题型:
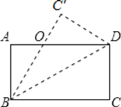
查看答案和解析>>【题目】如图所示,
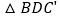 是将长方形纸牌ABCD沿着BD折叠得到的,图中
是将长方形纸牌ABCD沿着BD折叠得到的,图中 包括实线、虚线在内
包括实线、虚线在内 共有全等三角形______ 对
共有全等三角形______ 对
相关试题

