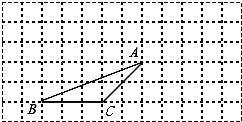
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
参考答案:
【答案】(1)见解析(2)平行且相等 ;(3)3
【解析】
(1)根据平移画图;
(2)由平移的性质得:AA′C′C,可得结论;
(3)如图3,画出高线AD,根据题意,利用三角形面积公式即可求得△ABC的面积.
解:(1)如图1,△A′B′C′即为所求;
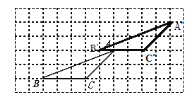
(2)AA',CC'的关系是平行且相等;
理由是:如图2,连接AA',CC',根据平移的性质可得:AA'=CC',AA'∥CC',
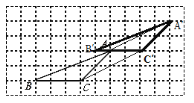
故答案为:相等且平行;
(3)如图3所示,AD即为所求.
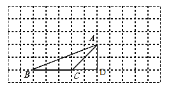
△ABC的面积=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC=90°,AB=4cm,BC=8cm,E、F是AD,DC的中点,连接EF、BE、BF,已知四边形ABCD的面积为36
 ,△DEF的面积是△DAC面积的
,△DEF的面积是△DAC面积的 ,求△BEF的面积_____
,求△BEF的面积_____ .
.
-
科目: 来源: 题型:
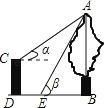
查看答案和解析>>【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,天星山山脚下西端A处与东端B处相距800(1+
 )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为  米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知EF⊥BC,AD⊥BC, ∠1=∠2,
⑴判断DM与AB的位置关系,并说明理由;
⑵若∠BAC=70°,DM平分∠ADC,求∠ACB的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 的图象与
的图象与 轴、
轴、 轴分别交于点
轴分别交于点 ,与函数
,与函数 的图象交于点
的图象交于点 ,点
,点 的横坐标为2.在
的横坐标为2.在 轴上有一点
轴上有一点 (其中
(其中 ),过点
),过点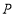 作
作 轴的垂线,分别交函数
轴的垂线,分别交函数 和
和 的图象于点
的图象于点 .
.(1)求点
 的坐标;
的坐标;(2)若四边形
 是平行四边形,求
是平行四边形,求 的值.
的值.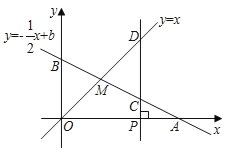
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

相关试题

