【题目】如图的中，，且为上一点．今打算在上找一点，在上找一点，使得与全等，以下是甲、乙两人的作法：

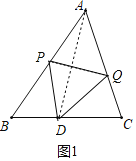
（甲）连接，作的中垂线分别交、于点、点，则、两点即为所求

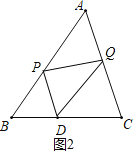
（乙）过作与平行的直线交于点，过作与平行的直线交于点，则、两点即为所求

对于甲、乙两人的作法，下列判断何者正确？（　　）

A. 两人皆正确B. 两人皆错误

C. 甲正确，乙错误D. 甲错误，乙正确

【答案】A

【解析】

如图1，根据线段垂直平分线的性质得到，，则根据“”可判断，则可对甲进行判断；

如图2，根据平行四边形的判定方法先证明四边形为平行四边形，则根据平行四边形的性质得到，，则根据“”可判断，则可对乙进行判断．

解：如图1，垂直平分，

，，

而，

，所以甲正确；

如图2，，，

∴四边形为平行四边形，

，，

而，

，所以乙正确．

故选：A．

关闭