Question

【题目】在等边△ABC中，AO是高，D为AO上一点，以CD为一边，在CD下方作等边△CDE，连接BE.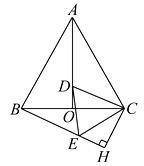

（1）求证：AD=BE；
（2）过点C作CH⊥BE，交BE的延长线于H，若BC＝8，求CH的长．

Answer 1

【答案】
（1）证明：∵△ABC和△CDE都是等边三角形，

∴CA=CB，CD=CE，∠ACB=60°，∠DCE=60°，

∴∠ACD+∠BCD=∠ACB=60°，∠BCE+∠BCD=∠DCE=60°，

∴∠ACD=∠BCE．

在△ACD和△BCE中，

，

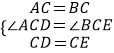∴△ACD≌△BCE（SAS）；

∴AD=BE

（2）解：∵△ABC是等边三角形，AO是BC边上的高，

∴∠BAC=60°，且AO平分∠BAC，

∴∠CAD= ∠BAC= ×60°=30°．

∵△ACD≌△BCE，

∴∠CAD=∠CBE，

∴∠CBE=30°．

又∵CH⊥BE，BC=8，

∴在Rt△BCH中，CH= BC= ×8=4，即CH=4

【解析】（1）根据等边三角形的性质得出CA=CB，CD=CE，∠ACB=60°，∠DCE=60°，从而得出∠ACD=∠BCE．然后利用SAS判断出△ACD≌△BCE ，根据全等三角形的性质得出AD=BE ；
（2）根据等腰三角形，底边上的三线合一得出∠CAD=30°．根据△ACD≌△BCE，得出∠CAD=∠CBE，从而得出∠CBE=30°．然后根据含30角的直角三角形的边角关系得出CH的长度。