【题目】抛物线y=2x2 , y=﹣2x2 , y=x2共有的性质是( )
A.开口向下
B.对称轴是y轴
C.都有最低点
D.y的值随x的增大而减小
参考答案:
【答案】B
【解析】解:∵y=2x2 , y= x2开口向上,∴A不正确,
∵y=﹣2x2 , 开口向下,∴有最高点,
∴C不正确,
∵在对称轴两侧的增减性不同,∴D不正确,
∵三个抛物线中都不含有一次项,
∴其对称轴为y轴,∴B正确,
故选B.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】两三角形的相似比为1∶4,它们的周长之差为27 cm,则较小三角形的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=
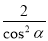 .
.上述结论中正确的个数是( )
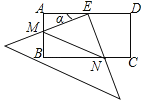
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4-0.5x)=15B.(x+3)(4+0.5x)=15
C.(x+4)(3-0.5x)=15D.(x+1)(4-0.5x)=15
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值不大于10.3的整数有( )
A. 10个 B. 11个 C. 20个 D. 21个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2+1的顶点坐标是( )
A.(2,1)
B.(0,1)
C.(1,0)
D.(1,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .

相关试题

