【题目】在如图的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上;
(1)建立适当的平面直角坐标系,使A(﹣2,﹣1),C(1,﹣1),写出B点坐标;
(2)在(1)的条件下,将△ABC向右平移4个单位再向上平移2个单位,在图中画出平移后的△A′B′C′,并分别写出A′、B′、C′的坐标;
(3)求△ABC的面积.

参考答案:
【答案】(1)点B的坐标为(0,1);(2)图形见解析,A′(2,1)、B′(4,3)、C′(5,1);(3)3
【解析】
(1)根据点A和点C的坐标可建立坐标系,结合坐标系得出点B的坐标;
(2)将三顶点分别向右平移4个单位再向上平移2个单位,得到对应点,顺次连接即可得;
(3)根据三角形的面积公式计算可得.
(1)如图所示,点B的坐标为(0,1);
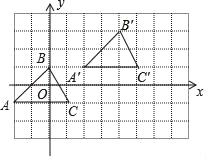
(2)如图所示,△A′B′C′即为所求,A′(2,1)、B′(4,3)、C′(5,1);
(3)△ABC的面积为![]() ×3×2=3.
×3×2=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内接于⊙O,如图所示,在劣弧
 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
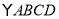 的面积为
的面积为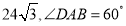 .点
.点 从点
从点 出发,以每秒
出发,以每秒 个单位的速度向点
个单位的速度向点 运动:点
运动:点 从点
从点 同时出发,以每秒
同时出发,以每秒 个单位的速度向点
个单位的速度向点 运动.规定其中一个点到达端点时,另一个点也随之停止运动。
运动.规定其中一个点到达端点时,另一个点也随之停止运动。 (1)求线段
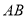 的长;
的长;(2)设点
 运动的时间为
运动的时间为 秒,当
秒,当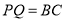 时,求
时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=
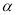 (
(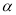 <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转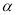 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF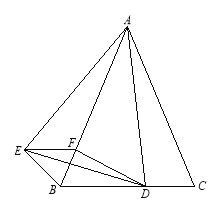
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(
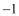 ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。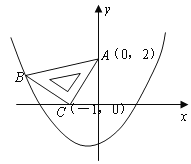
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
相关试题

