Question

【题目】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°

（1）请判断AB与CD的位置关系并说明理由；

（2）如图2，在（1）的结论下，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？

（3）如图3，在（1）的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？ （2、3小题只需选一题说明理由）

Answer 1

【答案】（1）AB∥CD；（2）∠BAE+∠MCD=90°；（3）∠BAC=∠PQC+∠QPC．

【解析】试题分析：（1）先根据CE平分∠ACD，AE平分∠BAC，得出∠BAC=2∠EAC，∠ACD=2∠ACE，再由可知故可得出结论；
（2）过E作EF∥AB，根据平行线的性质可知EF∥AB∥CD，∠BAE=∠AEF，∠FEC=∠DCE，故再由∠MCE=∠ECD，即可得出结论；
（3）根据AB∥CD， 可知 故∠BAC=∠PQC+∠QPC.

试题解析：(1)∵CE平分∠ACD，AE平分∠BAC，

∴∠BAC=2∠EAC，∠ACD=2∠ACE，

∵

∴

∴AB∥CD；

(2)

过E作EF∥AB，

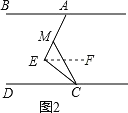
∵AB∥CD,

∴EF∥AB∥CD，

∴∠BAE=∠AEF，∠FEC=∠DCE，

∵

∴

∵∠MCE=∠ECD，

∴

(3)∵AB∥CD，

∴

∵

∴∠BAC=∠PQC+∠QPC.