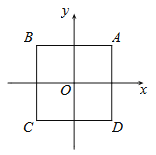
【题目】如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.
(1)若函数y=x2+m的图象过点C,求这个函数的解析式;并判断其函数图象是否过A点.
(2)若将(1)中的函数图象先向右平移1个单位,再向上平移2个单位,直接写出平移后函数的解析式和顶点坐标.
参考答案:
【答案】(1)y=x2﹣2,其函数图象不过A点;(2)平移后的抛物线的顶点坐标为(1,0).
【解析】试题分析:(1)根据题意A(1,1),C(-1,-1),代入y=x2+m根据待定系数法即可求得解析式,把A的坐标代入即可判断;
(2)直接利用抛物线平移规律:上加下减,左加右减进而得出平移后的解析式,即可得出顶点坐标.
试题解析:
(1),由题意得A(1,1),C(﹣1,﹣1),
∵函数y=x2+m的图象过点C,
∴﹣1=1+m,
解得m=﹣2,
∴此函数的解析式为y=x2﹣2,
把A(1,1)代入y=x2﹣2的左右两边,
左边=1,右边=﹣1,左≠右,
∴其函数图象不过A点.
(2)∵将抛物线y=x2﹣2向上平移2个单位再向右平移1个单位,
∴平移后的抛物线的解析式为:y=(x﹣1)2﹣2+2.
即y=(x﹣1)2,
则平移后的抛物线的顶点坐标为:(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动;第1次点A向左移动3个单位长度至点
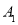 ,第2次从点
,第2次从点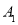 向右移动6个单位长度至点
向右移动6个单位长度至点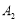 ,第3次从点
,第3次从点 向左移动9个单位长度至点
向左移动9个单位长度至点 ,…,按照这种移动方式进行下去,如果点
,…,按照这种移动方式进行下去,如果点 与原点的距离不小于20,那么n的最小值是________.
与原点的距离不小于20,那么n的最小值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
(1)当t= 时,△PQR的边QR经过点B;
(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;
(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.
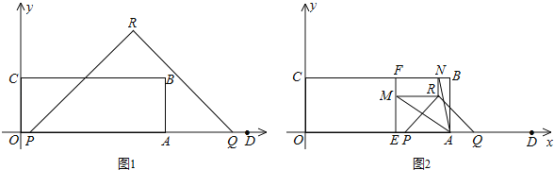
-
科目: 来源: 题型:
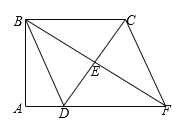
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一”儿童节促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料,再解答下列问题:
题:分解因式:
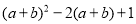
解:将“
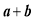 ”看成整体,设
”看成整体,设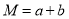 ,则原式=
,则原式=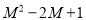
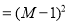
再将“
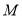 ”还原,得原式=
”还原,得原式=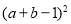 .
.上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:
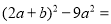 ;
;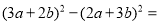 .
.(2)因式分解:
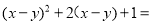 ;
;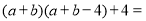 .
.(3)求证:若
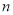 为正整数,则式子
为正整数,则式子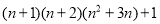 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方. -
科目: 来源: 题型:
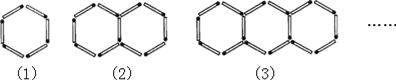
查看答案和解析>>【题目】用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,则第100个图形需要火柴棒________根.
相关试题

