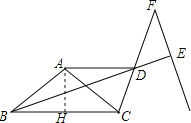
【题目】如本题图①,在△ABC中,已知∠ABC=∠ACB=α.过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求∠ACD的大小;
(2)在线段CD的延长线上取一点F,以FD为角的一边作∠DFE=α,另一边交BD延长线于点E,若FD=kAD(如本题图②所示),试求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).

参考答案:
【答案】(1)∠ACD=90°﹣![]() ;(2)
;(2)![]() =
=![]() k2.
k2.
【解析】试题分析:(1)由∠ABC=∠ACB,BD平分∠ABC,得到∠1=∠2=![]() ,AB=AC,因为AD∥BC,推出∠2=∠3,得到∠3=∠1=
,AB=AC,因为AD∥BC,推出∠2=∠3,得到∠3=∠1=![]() ,得到AB=AD.AC=AD=AB.于是得到∠ACD=∠ADC=
,得到AB=AD.AC=AD=AB.于是得到∠ACD=∠ADC=![]() ,根据AD∥BC,∠CAD=ACB=α,得出结论∠ACD=∠ADC=
,根据AD∥BC,∠CAD=ACB=α,得出结论∠ACD=∠ADC=![]() =90°﹣
=90°﹣![]() .
.
(2)过A作AH⊥BC于点H,得到∠AHB=90°.证出∠BAH=90°﹣α,因为AD∥BC,得出∠BDC+∠ADC=180°,然后证得对应角相等,得到相似三角形,根据相似三角形的性质得比例式求得结果.
试题解析:(1)∵∠ABC=∠ACB,BD平分∠ABC,∴∠1=∠2=![]() ,AB=AC,
,AB=AC,
∵AD∥BC,∴∠2=∠3,∴∠3=∠1=![]() ,∴AB=AD.
,∴AB=AD.
∴AC=AD=AB.∴∠ACD=∠ADC=![]() ,
,
又∵AD∥BC,∴∠CAD=ACB=α,
∴∠ACD=∠ADC=![]() =90°﹣
=90°﹣![]() ;
;
(2)过A作AH⊥BC于点H,则∠AHB=90°.
∴∠BAH=90°﹣α,
∵AD∥BC,∴∠BDC+∠ADC=180°,即:∠BCA+∠ACD+∠CDB+∠3=180°,
由∠ACB=α,∠ACD=90°﹣![]() ,∠3=
,∠3=![]() ,
,
得:∠CDB=180°﹣α﹣(90°﹣![]() )﹣
)﹣![]() =90°﹣α.
=90°﹣α.
∴∠FDE=∠CDB=90°﹣α,∴∠BAH=∠FDE,∵∠ABH=∠DFE=α,
∴△ABH∽△DEF,
∵FD=kAD,AB=AD,∴S△DEF=k2S△BAH,
∵AD∥BC,∴S△BCD=S△ABC=2S△BAH,∴![]() =
=![]() k2,
k2,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

-
科目: 来源: 题型:
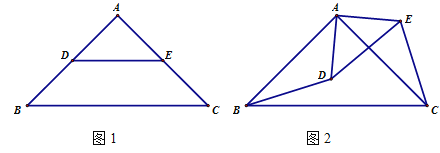
查看答案和解析>>【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
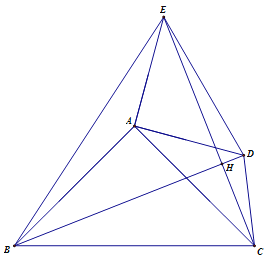
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=
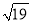 ,求四边形BCDE的面积;
,求四边形BCDE的面积;②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面坐标坐标系
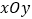 中,点
中,点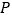 的坐标为
的坐标为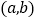 ,点
,点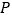 的变换点
的变换点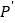 的坐标定义如下:当
的坐标定义如下:当 时,点
时,点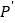 的坐标为
的坐标为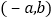 ;当
;当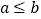 时,点
时,点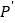 的坐标为
的坐标为 .
.已知点
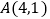 ,点
,点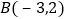 ,点
,点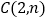 .
.(
 )点
)点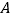 的变换点
的变换点 的坐标是__________.
的坐标是__________.点
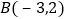 的变换点为
的变换点为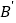 ,连接
,连接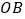 ,
,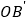 ,则
,则 __________.
__________.(
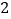 )点
)点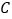 的变换点为
的变换点为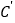 ,随着
,随着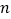 的变化,点
的变化,点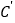 会运动起来,请在备用图(
会运动起来,请在备用图(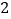 )中画出点
)中画出点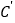 的运动路径.
的运动路径.(
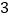 )若
)若 是等腰三角形,请直接写出此时
是等腰三角形,请直接写出此时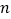 的值:__________.
的值:__________.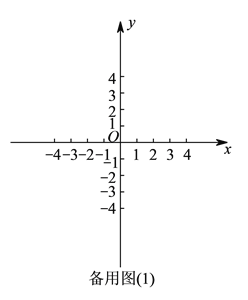

-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B在第_____象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3
相关试题

