【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 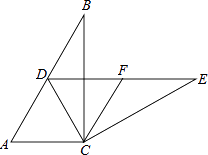
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
参考答案:
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,
∴AC=DC,∠A=60°,
∴△ADC是等边三角形,
∴∠ACD=60°,
∴n的值是60
(2)解:四边形ACFD是菱形;
理由:∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形
【解析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(2,3),B(1,1),C(4,1),M(6,3).
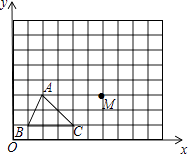
(1)将△ABC平原得到△A1B1C1 , 其中点A,B,C的对应点分别是A1 , B1 , C1 , 且点A1的坐标是(3,6),在图中画出△A1B1C1 .
(2)将(1)中的△A1B1C1绕点M顺时针旋转90°,画出旋转后的△A2B2C2(其中点A2 , B2 , C2的对应点分别是A1 , B1 , C1),并写出点A2 , B2 , C2的坐标.
(3)(2)中的△A2B2C2能通过旋转△ABC得到吗?若能,请写出旋转的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E. 求证:AB=BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据绘制如下的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)
(1)直接写出y与x之间的函数解析式;
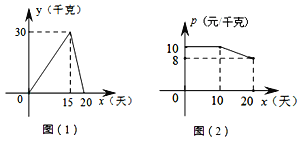
(2)分别求第10天和第15天的销售额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中,“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.

①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )

A. 5cm B. 6cm C. 7cm D. 8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
相关试题

